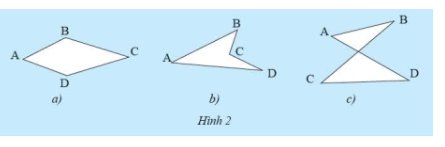
Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)