\(a)\sqrt {2250} \approx 47,434;\,\,\,\,\,\,b)\sqrt {12} \approx 3,461;\,\,\,\,\,\,\,c)\sqrt 5 \approx 2,236\,\,\,\,\,\,\,\,\,d)\sqrt {624} \approx 24,980\)
Dùng máy tính cầm tay để tính các căn bậc hai số học sau:
\(\sqrt 3 ;\,\sqrt {15\,\,129} ;\,\sqrt {10\,\,000} ;\,\sqrt {10} \).
Tính:
\(a)\sqrt {64} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b)\sqrt {{{25}^2}} ;\,\,\,\,\,\,\,\,\,\,\,c)\sqrt {{{\left( { - 5} \right)}^2}} .\)
Tính bán kính của một hình tròn có diện tích là 9869 m2 (dùng máy tính cầm tay).
Chọn phát biểu đúng trong các phát biểu sau:
\(a)\sqrt 2 \in I;\,\,\,\,\,b)\sqrt 9 \in I;\,\,\,\,c)\,\pi \in I;\,\,\,\,\,d)\sqrt 4 \in \mathbb{Q}\)
Tìm số hữu tỉ trong các số sau:
\(12;\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{2}{3};\,\,\,\,\,\,3,\left( {14} \right);\,\,\,\,\,\,\,0,123;\,\,\,\,\,\,\,\,\sqrt 3 \)
a) Sử dụng máy tính cầm tay bấm liên tiếp các nút
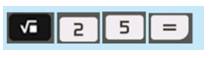
Em hãy đọc kết quả x trên màn hình rồi tính x2.
b) Sử dụng máy tính cầm tay bấm liên tiếp các nút
Em hãy đọc kết quả x trên màn hình rồi tính x2.
Hãy thực hiện các phép chia sau đây:
\(3:2 = ?\,\,\,\,\,\,\,\,\,\,\,37:25 = ?\,\,\,\,\,\,\,\,5:3 = ?\,\,\,\,\,\,1:9 = ?\)
b) Dùng kết quả trên để viết các số \(\frac{3}{2};\frac{{37}}{{25}};\frac{5}{3};\frac{1}{9}\) dưới dạng số thập phân.
Dùng máy tính cầm để:
a) Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 12 996 m2
b) Công thức tính diện tích S của hình tròn bán kính R là \(S = \pi {R^2}\). Tính bán kính của một hình tròn có diện tích là 100 cm2.
a) Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân:
\(\frac{{15}}{8};\,\,\,\frac{{ - 99}}{{20}};\,\,\,\frac{{40}}{9};\,\,\, - \frac{{44}}{7}\)
b) Trong các số thập phân vừa tính được, hãy chỉ ra các số thập phân vô hạn tuần hoàn.
