\(a,\dfrac{\pi}{12}=\dfrac{180\cdot\dfrac{\pi}{12}}{\pi}=15^o\\ b,-5=\dfrac{-180\cdot5}{\pi}=\left(-\dfrac{900}{\pi}\right)^o\\ c,\dfrac{13\pi}{9}=\dfrac{180\cdot\dfrac{13\pi}{9}}{\pi}=260^o\)
Bài 1. Góc lượng giác Toán
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Đổi số đo của các góc sau đây sang radian
a) \(38^\circ \)
b) \( - 115^\circ \)
c) \({\left( {\frac{3}{\pi }} \right)^\circ }\)
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:Số đo theo độ0°?45°60°?120°?150°180°Số đo theo rad?frac{pi }{6}(rad)??frac{pi }{2}(rad)?frac{{3pi }}{4}(rad)?pi (rad)
Đọc tiếp
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:
Số đo theo độ | 0° | ? | 45° | 60° | ? | 120° | ? | 150° | 180° |
Số đo theo rad | ? | \(\frac{\pi }{6}(rad)\) | ? | ? | \(\frac{\pi }{2}(rad)\) | ? | \(\frac{{3\pi }}{4}(rad)\) | ? | \(\pi (rad)\) |
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
a) \(\frac{{ - 17\pi }}{3}\)
b) \(\frac{{13\pi }}{4}\)
c) \( - 765^\circ \)
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?frac{pi }{2} + kfrac{{2pi }}{3},,left( {k in mathbb{Z}} right);frac{{ - pi }}{6} + kfrac{{2pi }}{3},,left( {k in mathbb{Z}} right);frac{pi }{2} + kfrac{pi }{3},,left( {k in mathbb{Z}} right)
Đọc tiếp
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?
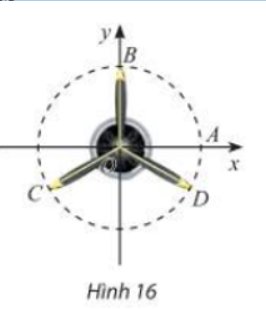
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:
a) \(\frac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)\)
b) \(k\frac{\pi }{4}\,\,\left( {k \in Z} \right)\)
Góc lượng giác \(\frac{{31\pi }}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
\(\frac{{3\pi }}{7};\,\,\frac{{10\pi }}{7};\,\,\frac{{ - 25\pi }}{7}\)
Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:
a) \( - {1485^ \circ }\)
b) \(\frac{{19\pi }}{4}\)
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)^\circ }\) của đường kinh tuyến (Hình 17). Đổi số đo \(\alpha \) sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilomet, biết bán kính trung bình của Trái Đất là 6371km. Làm tròn kết quả đến hàng phần trăm.
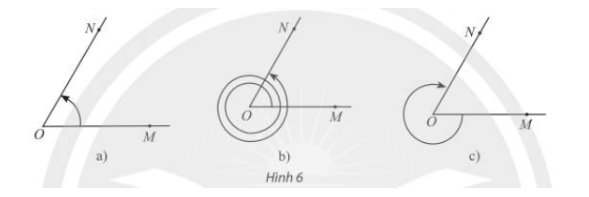
Cho \(\widehat {MON} = {60^ \circ }\). Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM,ON).