Vì cộng cả tử và mẫu của phân số \(\dfrac{23}{40}\) với cùng một số tự nhiên n rồi rút gọn ta được \(\dfrac{3}{4}\) nên ta được:
\(\dfrac{23+n}{40+n}=\dfrac{3}{4}\)
\(\Rightarrow\)\(4.\left(23+n\right)=3.\left(40+n\right)\)
hay 92 + 4.n = 120 + 3.n
4.n - 3.n = 120 - 92
\(\Rightarrow\) n = 28
Vậy số tự nhiên n cần tìm là 28
Ta có phân số mới: \(\dfrac{23+n}{40+n}\) (n ∈ N)
Theo bài ra ta có: \(\dfrac{23+n}{40+n}\)=\(\dfrac{3}{4}\)
Nên (23+n).4=3.(40+n)
⇒⇒ 92+4n = 120+3n
⇒⇒ 4n-3n= 120-92
⇒⇒ n = 28
Vậy \(\dfrac{23+28}{40+28}\)=\(\dfrac{51}{68}\)=\(\dfrac{3}{4}\)
Theo đề bài, ta có: 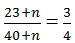
⇔ 4(23 + n) = 3 (40 + n) ⇔ 4n + 92 = 120 + 3n
⇔ 4n – 3n = 120 – 92 ⇔n = 28
Vậy n = 28.








