a) Lượng nước chảy vào bể sau 1 giờ là:
\(1.2 = 2\left( {{m^3}} \right)\)
b) Lượng nước chảy vào bể sau \(x\) giờ là:
\(2.x = 2x\left( {{m^3}} \right)\)
c) Lượng nước \(y\) có trong bể sau \(x\) giờ là:
\(y = 2x + 5\left( {{m^3}} \right)\).
a) Lượng nước chảy vào bể sau 1 giờ là:
\(1.2 = 2\left( {{m^3}} \right)\)
b) Lượng nước chảy vào bể sau \(x\) giờ là:
\(2.x = 2x\left( {{m^3}} \right)\)
c) Lượng nước \(y\) có trong bể sau \(x\) giờ là:
\(y = 2x + 5\left( {{m^3}} \right)\).
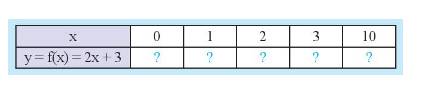
Lượng nước \(y\) (tính theo \({m^3}\)) có trong một bể nước sau \(x\) giờ mở vòi cấp nước được cho bởi hàm số \(y = 2x + 3\). Tính lượng nước có trong bể sau 0 giờ; 1 giờ; 2 giờ; 3 giờ; 10 giờ và hoàn thành bảng giá trị sau:
Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là 10 cm. Cho biết treo thêm vào lò xo 1 vật nặng 1 kg thì chiều dài lò xo tăng thêm 3 cm.
a) Tính chiều dài \(y\) (cm) của lò xo theo khối lượng \(x\) (kg) của vật.
b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).
Với giá trị nào của \(m\) thì mỗi hàm số sau đây là hàm số bậc nhất?
a) \(y = \left( {m - 1} \right)x + m\); b) \(y = 3 - 2mx\).
Một hình chữ nhật có các kích thước là \(2m\) và \(3m\). Gọi \(y\) là chu vi của hình chữ nhật này sau khi tăng chiều dài và chiều rộng thêm \(x\left( m \right)\). Hãy chứng tỏ \(y\)là một hàm số bậc nhất theo biến số \(x\). Tìm các hệ số \(a;b\) của hàm số này.
Lập bảng giá trị của mỗi hàm số bậc nhất sau:
\(y = f\left( x \right) = 4x - 1\) và \(y = h\left( x \right) = - 0,5x + 8\) với \(x\) lần lượt bằng –3; –2; –1; 0; 1; 2; 3.
Tìm các hàm số bậc nhất trong các hàm số sau đây và chỉ ra các hệ số \(a,b\) của các hàm số đó:
\(y = 4x - 7\);\(y = {x^2}\);\(y = - 6x - 4\);\(y = 4x\);\(y = \dfrac{3}{x}\);\(s = 5v + 8\);\(m = 30n - 25\).
Một xe khách khởi hành từ bến xe phía Bắc bưu điện thành phố Nha Trang để đi ra thành phố Đà Nẵng với tốc độ 40 km/h (Hình 2).

a) Biết rằng bến xe cách bưu điện thành phố Nha Trang 6 km. Sau \(x\) giờ, xe khách cách bưu điện thành phố Nha Trang \(y\)km. Tính \(y\) theo \(x\).
b) Chứng minh rằng \(y\) là một hàm số bậc nhất theo biến \(x\).
c) Hoàn thành bảng giá trị của hàm số ở câu b) và giải thích ý nghĩa của bảng giá trị này:
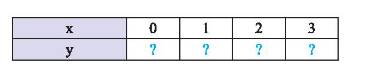
a)
Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:
\(y = x\); \(y = x + 2\); \(y = - x\) \(y = - x + 2\).
Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số \(a,b\) của chúng.
a) \(y = 4x + 2\); b) \(y = 5 - 3x\); c) \(y = 2 + {x^2}\);
d) \(y = - 0,2x\); e) \(y = \sqrt 5 x - 1\).