a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB - AE = 12 - 8 = 4cm
∆ADE ∽ ∆BFE => \(\dfrac{AE}{BE}=\dfrac{AD}{BF}=\dfrac{DE}{FD}\)
=> \(\dfrac{8}{4}=\dfrac{7}{BF}=\dfrac{10}{EF}\)
=> BF = 3,5 cm.
EF = 5 cm.
a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB - AE = 12 - 8 = 4cm
∆ADE ∽ ∆BFE => \(\dfrac{AE}{BE}=\dfrac{AD}{BF}=\dfrac{DE}{FD}\)
=> \(\dfrac{8}{4}=\dfrac{7}{BF}=\dfrac{10}{EF}\)
=> BF = 3,5 cm.
EF = 5 cm.
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k ?
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k
Tam giác vuông ABC có \(\widehat{A}=90^0\) và đường cao AH. Từ điểm H hạ đường HK vuông góc với AC (h.27)
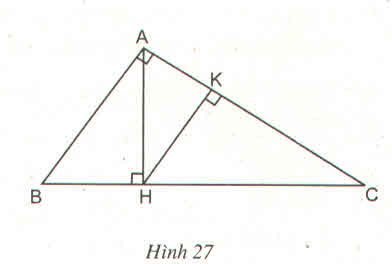
a) Hỏi trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau ?
b) Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng ?
Hai ∆ đồng dạng thì mình có được tỉ số đồng dạng đúng kh
Cho tam giác ABC AB<AC trên cạnh AC lấy điểm D sao cho góc ABD=góc ACB
1) chứng minh rằng tam giác ABD đồng dạng với tam giác ACB viết tỉ số đồng dạng
2) chứng minh rằng AB\(^2\)=AD.AC
Cho Tam giác ABC đồng dạng với DEF. Gọi M,N lần lượt là trung điểm của BC,EF. Chứng minh 2 tam giác ABM đồng dạng với Tam giác DEN và AC/DF=AM/DN
Cho tam giác ABC vuông góc tại A, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. a, Chứng minh AH = MN b, Chứng minh tam giác AHM đồng dạng với tam giác AHB rồi suy ra AH^2 = AM . AB c, Chứng minh tam giác AMN đồng dạng với tam giác ACB d, Cho AB = 6cm, AC = 8cm. Tính diện tích của tam giác AMN.
cho tam giác abc đồng dạng với tam giác a'b'c' gọi ah ad am lần lượt là đường cao phân giác trung tuyến xuất phát từ dỉnh a của tam giác abc ah' ad' am' lần lượt là đường cao phân giác trung tuyến xuất phát từ dỉnh a của tam giác a'b'c' chứng minh ràng tam giác abh đồng dạng vớ tam giác a'b'h'
cho tam giác ABC vuông tại A có AB=6cm ,AC=8cm. đường cao AH và phân giác BDcắt nhau tại I (H trên BC và D trên AC)
a)tính độ dài AD,DC
b)Chướng minh tam giác ABC đồng dạng tam giác HBA và AB2=BH.BC
c)chứng minh tam giác ABI đồng dang với tam giác CBD