Bài 7: Trường hợp đồng dạng thứ ba
Các câu hỏi tương tự
Chứng minh rằng, nếu hai tam giác ABC và A'B'C' đồng dạng với nhau thì :
a) Tỉ số của hai đường phân giác tương ứng bằng tỉ số đồng dạng
b) Tỉ số của hai trung tuyến tương ứng bằng tỉ số đồng dạng
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k ?
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k
Cho DeltaABC có 3 góc nhọn (ABAC).Kẻ các đường cao AD,BE,CF cắt nhau tại H.Chứng minh:a) DeltaABE đồng dạng với DeltaACFb) AF.ABAE.ACc) DeltaAEF đồng dạng với DeltaABCd) DeltaEBC đồng dạng với DeltaDACe) EH là phân giác của góc DEF
Đọc tiếp
Cho \(\Delta\)ABC có 3 góc nhọn (AB<AC).Kẻ các đường cao AD,BE,CF cắt nhau tại H.Chứng minh:
a) \(\Delta\)ABE đồng dạng với \(\Delta\)ACF
b) AF.AB=AE.AC
c) \(\Delta\)AEF đồng dạng với \(\Delta\)ABC
d) \(\Delta\)EBC đồng dạng với \(\Delta\)DAC
e) EH là phân giác của góc DEF
Cho tam giác ABC AB<AC trên cạnh AC lấy điểm D sao cho góc ABD=góc ACB
1) chứng minh rằng tam giác ABD đồng dạng với tam giác ACB viết tỉ số đồng dạng
2) chứng minh rằng AB\(^2\)=AD.AC
Tìm các dấu hiệu để nhận biết hai tam giác cân đồng dạng ?
cho tam giác ABC có ba góc nhọn. Gọi O là giao điểm của ba đường cao AH, BK, CI. chứng minh:
a, OK.OB = OI.OC
b, tam giác OIB đồng dạng với tam giác OKC
c, tam giác BOH đồng dạng với tam giác BCK
d, BO.BK + CO.CI = BC2
Tam giác vuông ABC có widehat{A}90^0 và đường cao AH. Từ điểm H hạ đường HK vuông góc với AC (h.27)
a) Hỏi trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau ?
b) Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng ?
Đọc tiếp
Tam giác vuông ABC có \(\widehat{A}=90^0\) và đường cao AH. Từ điểm H hạ đường HK vuông góc với AC (h.27)
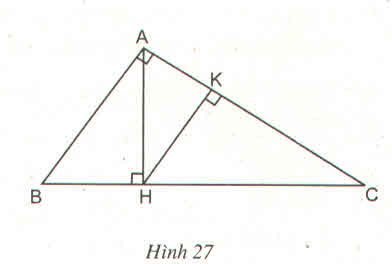
a) Hỏi trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau ?
b) Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng ?
Hình bs.5 cho biết tam giác ABC có hai đường cao AD và BE cắt nhau tại H
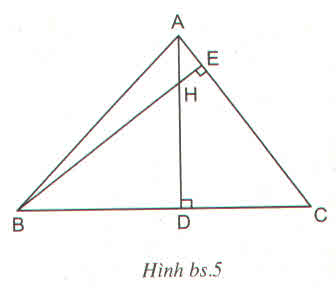
Trong hình bs.5 có số cặp tam giác đồng dạng với nhau là :
(A) 1 cặp
(B) 2 cặp
(C) 3 cặp
(D) 4 cặp
Hãy chọn kết quả đúng ?










