Bài 12: Dấu hiệu chia hết cho 3, cho 9
Các câu hỏi tương tự
Một số có tổng các chữ số chia cho 9 (cho 3) dư m thì số đó chia cho 9 (cho 3) cũng dư m
Ví dụ :
Số 1543 có tổng số các chữ số bằng : \(1+5+4+3=13\). Số 13 chia cho 9 dư 4, chia 3 dư 1. DO đó số 1543 chia 9 dư, chua 3 dư 1
Tìm số dư khi chia mỗi số sau cho 9, cho 3 : 1546; 1527; 2468; \(10^{11}\)
Câu 1. Chọn khẳng định đúng trong các khẳng định dưới đây:
A. Những số chia hết cho 9 thì chia hết cho 3
B. Những số chia hết cho 3 thì chia hết cho 9
C. Những số có chữ số tận cùng là 3 thì chia hết cho 3
D. Những số có chữ số tận cùng là 3 hoặc 9 thì chia hết cho 9
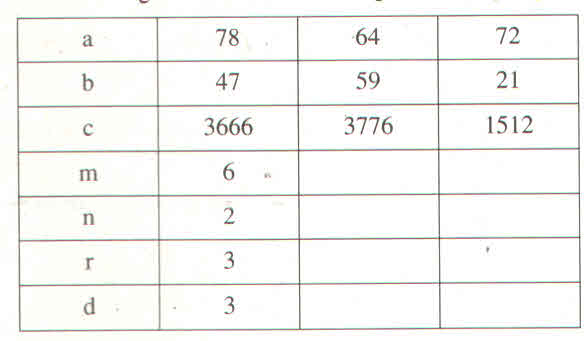
Trong phép nhân \(a.b=c\) gọi :
m là số dư của a khi chia cho 9, n là số dư của b khi chia cho 9
r là số dư của tích m.n khi chia cho 9, d là số dư của c khi chia cho 9
Điền vào các ô trống rồi so sánh r và d trong mỗi trường hợp sau :
số tự nhiên nhỏ nhất chia hết cho 9 , chia 5 dư 3 và chia 2 dư 1
Dùng 3 trong bốn chữ 4, 5, 3, 0 hãy ghép thành các số tự nhiên có ba chữ số sao cho các số đó :
a) Chia hết cho 9
b) Chia hết cho 3 mà không chia hết cho 9
Dùng ba trong bốn chữ số 7, 6, 2, 0 hãy ghép thành các số tự nhiên có ba chữ số sao cho số đó :
a) Chia hết cho 9
b) Chia hết cho 3 mà không chia hết cho 9
ae cho tôi hỏi :
một số có 3 chữ số và chữ số đầu là 3 thì làm thế nào để cả 3 số đó chia hết cho cả 3 , 6 , 9
chứng minh rằng hiệu của một số và tổng các chữ số của nó chia hết cho 9
1) Tìm các số tự nhiên có ba chữ số, biết rằng khi chia số đó cho 25; 28; 35 thì được số dư lần lượt là 3; 6; 13. 2)Tìm số nguyên tố n để n + 10; n + 14 cũng là các số nguyên tố. 3) Trong một cuộc thi có 20 câu hỏi, mỗi câu trả lời đúng được 10 điểm, mỗi câu trả lời sai không những không được điểm nào mà còn bị trừ 5 điểm. Một học sinh dự thi được 125 điểm. Hỏi bạn đó đã trả lời đúng mấy câu? giúp mk với
Đọc tiếp
1) Tìm các số tự nhiên có ba chữ số, biết rằng khi chia số đó cho 25; 28; 35 thì được số dư lần lượt là 3; 6; 13.
2)Tìm số nguyên tố n để n + 10; n + 14 cũng là các số nguyên tố.
3) Trong một cuộc thi có 20 câu hỏi, mỗi câu trả lời đúng được 10 điểm, mỗi câu trả lời sai không những không được điểm nào mà còn bị trừ 5 điểm. Một học sinh dự thi được 125 điểm. Hỏi bạn đó đã trả lời đúng mấy câu?
giúp mk với







