Question

Cho vecto \(\overrightarrow {AB}  = \overrightarrow a \). Hãy xác định điểm C sao cho \(\overrightarrow {BC}  = \overrightarrow a \)

a) Tìm mối quan hệ giữa \(\overrightarrow {AB} \) và \(\overrightarrow a  + \overrightarrow a \)

b) Vecto \(\overrightarrow a  + \overrightarrow a \) có mối quan hệ như thế nào về hướng và độ dài đối với vecto \(\overrightarrow a \)

Answer 1

Tham khảo:

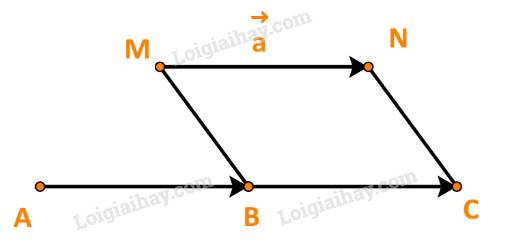
Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).

Từ B, M, N ta dựng hình bình hành BMNC.

Khi đó: \(\overrightarrow {MN}  = \overrightarrow {BC} \) hay \(\overrightarrow a  = \overrightarrow {BC} \).

\( \Rightarrow \overrightarrow a  + \overrightarrow a  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

a) Vì  \(\overrightarrow {AB}  = \overrightarrow a  = \overrightarrow {BC} \) nên A, B, C thẳng hàng và B là trung điểm của AC.

Vậy \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)

b) Ta có:  \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)

Mà \(\overrightarrow {AB}  = \overrightarrow a \) nên:  \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow a \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow a } \right|\).