Question

Cho tứ diện ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD)

a) Chứng minh H là tâm đường tròn ngoại tiếp tam giác BCD. Tính độ dài đoạn AH

b) Tính diện tích xung quanh và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác BCD và chiều cao AH

Answer 1

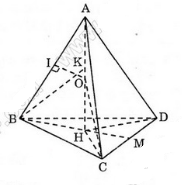
a,+) Từ A vẽ AH _|_ (BCD) (theo giả thiết AB = AC = AD)

Nên \(\Delta ABH=\Delta ACH=\Delta ADH\)

=> HB = HC = HD

Vậy H là tâm đường tròn ngoại tiếp tam giác BCD

+) Ta có: \(AH=\sqrt{AB^2-BH^2}\) với \(BH=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot\dfrac{a\sqrt{3}}{3}\)

\(\Rightarrow AH=\sqrt{a^2-\dfrac{3a^2}{9}}=\dfrac{a\sqrt{6}}{3}\)

b, Ta có: \(H=AH=\dfrac{a\sqrt{6}}{3};r=BH=\dfrac{a\sqrt{3}}{3}\)

Diện tích xung quanh hình trụ là:

\(S_{xq}=2\pi rh=2\pi.\dfrac{a\sqrt{3}}{3}.\dfrac{a\sqrt{6}}{3}=\dfrac{2\pi\pi^2\sqrt{2}}{3}\)

Thể tích khối trụ là:

\(V=\pi r^2h=\pi\left(\dfrac{a\sqrt{3}}{3}\right)^2.\dfrac{a\sqrt{6}}{3}=\dfrac{\pi a^3\sqrt{6}}{9}\)