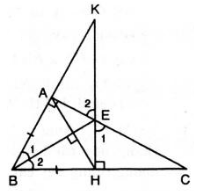
a,Xét tam giác ABE và tam giác HBE có :
BE chung;góc ABE=HBE(BE là tia p/g)
Suy ra 2 tam giác trên bằng nhau theo trường hợp (ch-gn)
b,Ta có BA=BH(2 tam giác trên bằng nhau)
suy ra B thuộc đường trung trực của AH (1)
EA=EH
suy ra E thuộc đường trung trực của AH (2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c,Xét tam giác EAK và tam giác EHC có :
góc AEK=HEC(đối đỉnh);góc EAK=EHC(=90);AE=EH(cmt)
Suy ra 2 tam giác đó = nhau theo trường hợp (g.c.g)
suy ra EK=EC
d,Trong tam giác EHC có góc EHC=90 ,do góc vuông là góc lớn nhất nên cạnh huỳen là cạnh lớn nhất
suy ra HE nhỏ hơn EC (3)
Mà AE=HE(tam giác EAK=EHC) (4)
Từ (3) và (4) suy ra AE nhỏ hơn EC
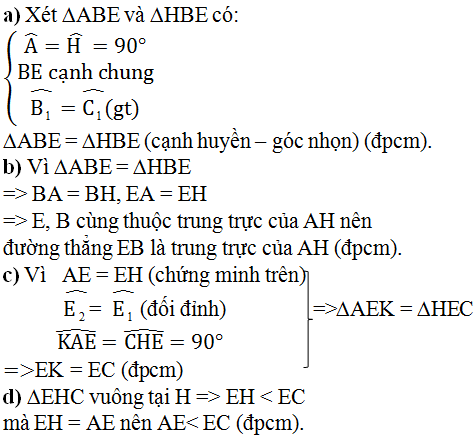
a)∆ABE = ∆HBE
Xét hai tam giác vuông ∆ABE và ∆HBE, ta có:
ˆB1=ˆB2B1^=B2^ (do BE là phân giác của góc B)
BE : cạnh huyền chung
Vậy ∆ABE = ∆HBE (g.c.g)
b) Chứng minh BE là đường trung trực của đoạn thẳng AH.
Vì ∆ABE = ∆HBE
=>BA = BH, EA = EH
=>E, B cùng thuộc trung trực của AH nên đường thẳng EB là trung trực của AH.
c) EK = EC.
Xét 2 tam giác ∆AEK và ∆HEC , ta có: ˆH=ˆA=900H^=A^=900
EA = EH (chứng minh trên)
ˆE2=ˆE1E2^=E1^ (đối đỉnh)
Vậy ∆AEK = ∆HEC => EK = EC (đpcm)
Trong tam giác vuông AEK ta có:
AE < EK (cạnh huyền lớn hơn cạnh góc vuông)
Mà EC = EK. Suy ra EC < EK (đpcm)