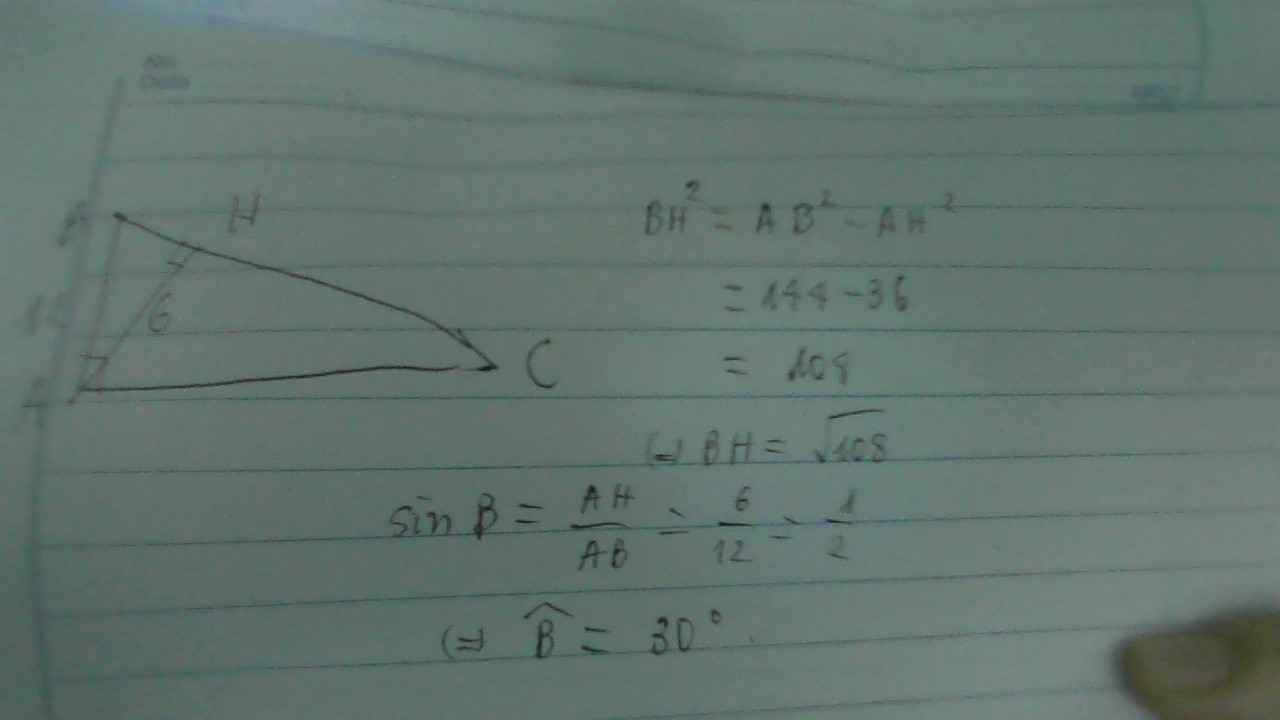\(sinB=\dfrac{\text{a}h}{\text{a}b}=\dfrac{6}{12}=>gocB=30^o\)
ap dụng Pytago vs tam giac BHa
\(BH^2+H\text{a}^2=\text{a}b^2=>BH=\sqrt{\text{a}b^2-\text{a}h^2}=\sqrt{12^2-6^2}=6\sqrt{3}\left(cm\right)\)
Xét \(\Delta ABH\) vuông tại A:
\(AB^2=AH^2+BH^2\left(Pytago\right).\\ 12^2=6^2+BH^2.\\ BH^2=108.\\ \Rightarrow BH=6\sqrt{3}.\)
\(\sin B=\dfrac{AH}{AB}.\\ \sin B=\dfrac{6}{12}.\\ \Rightarrow\widehat{B}=30^o.\)