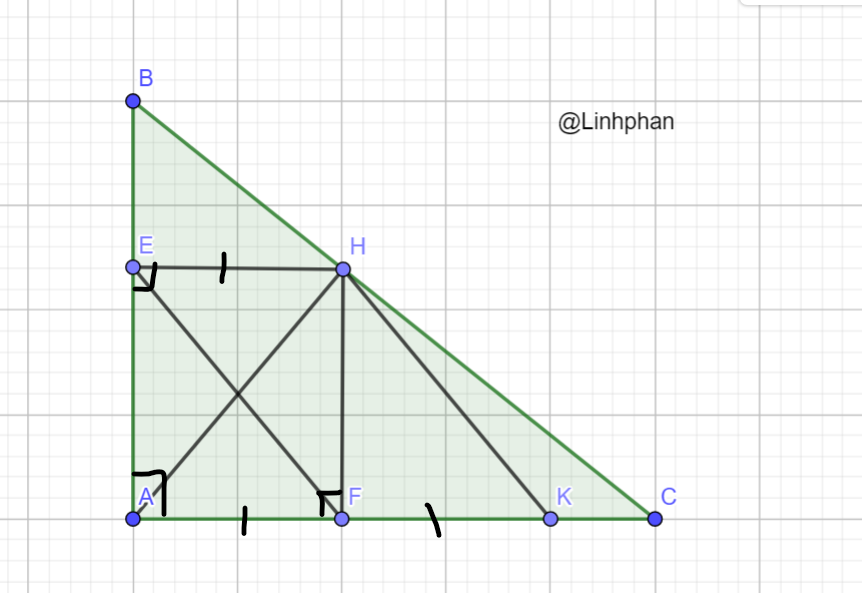
a, Vì HE ⊥ AB ; FA ⊥ AB => HE // FA (từ ⊥ đến // )
+, EA ⊥ AC ; HF ⊥ AC => EA // HF (từ ⊥ đến // )
Xét tứ giác AEHF có: HE // FA (cmt) ; EA // HF (cmt)
=> Tứ giác AEHF là hình bình hành (dhnb)
mà \(\hat{EAF} =90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> AH = EF
b, Vì AEHF là hình chữ nhật (cmt)
=> EH//AF; EH = AF mà AF= FK (gt)
=> EH = FK
+, Xét tứ giác EHKF có: EH = FK (cmt)
EH // FK (do EH // AF; K ∈ AF)
=> Tứ giác EHKF là hình bình hành (dhnb)











