vẽ đường cao AH chung của tam giác AMB và AMC
SAMB=\(\dfrac{1}{2}\)BM.AH
SAMC=\(\dfrac{1}{2}\)CM.AH
Vì AM là đường trung tuyến nên BM=MC
Do đó:SAMC=SAMB
( cái đường cao AH vuông góc với BC ă)
vẽ đường cao AH chung của tam giác AMB và AMC
SAMB=\(\dfrac{1}{2}\)BM.AH
SAMC=\(\dfrac{1}{2}\)CM.AH
Vì AM là đường trung tuyến nên BM=MC
Do đó:SAMC=SAMB
( cái đường cao AH vuông góc với BC ă)
Cho tam giác ABC có 2 đường trung tuyến AM và BN vuông góc với nhau. Tính diện tich tam giác ABC theo AM và BN
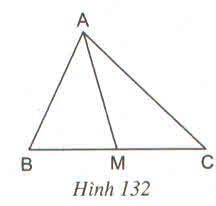
Cho tam giác ABC và đường trung tuyến AM (h.132)
Chứng minh :
\(S_{AMB}=S_{AMC}\)
Cho tam giác ABC vuông tại A biết AB=6cm, AC=8cm, đường cao AH. Gọi D,E lần lượt là chân đường vuông góc kẻ từ H đến AB và AC.
a, Tính diện tích tam giác ABC.
b, Chứng minh AH=DE
c, Kẻ trung tuyến AM của tam giác ABC. Chứng minh rằng AM vuông góc với AD
Cho tam giác ABC có AM là trung tuyến. CMR: SABM=SACM.
Cho tam giác ABC,trung tuyến AM.Gọi I là trung điểm của AM,tia BI cắt AC tại D,tia CI cắt AB tại E.Tính diện tích tam giác AID biết diện tích tam giác ABC=30cm2
Tam giác ABC vuông tại A có AB = 8cm; AC = 9cm, đường trung tuyến AM. Khi đó diện tích tam giác ABM bằng:
72 mét vuông
36 mét vuông
18 mét vuông
9 mét vuông
Cho \(\Delta\)ABC,các đường trung tuyến AM,BE,CF cắt nhau tại G
a)Chứng minh:S\(\Delta\)BAG=\(\dfrac{1}{3}\)S\(\Delta\)ABC
b)Chứng minh S\(\Delta\)ABG=S\(\Delta\)ACG=S\(\Delta\)BCG