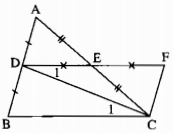
a) Xét ∆ADE và ∆CFE, ta có:
AE = CE (gt)
ˆAED = CEF^ (đối đỉnh)
DE = FE(gt)
Suy ra: ∆ADE = ∆CFE (c.g.c)
⇒⇒ AD = CF (hai cạnh tương ứng)
Mà AD = DB (gt)
Vậy: DB = CF
b) Ta có: ∆ADE = ∆CFE (chứng minh trên)
⇒ˆADE = CFE^ (2 góc tương ứng)
⇒⇒ AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ∆DBC = ∆CDF, ta có:
BD = CF (chứng minh trên)
ˆBDC = ˆFCD (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ∆BDC = ∆FCD(c. g. c)
c) Ta có: ∆BDC = ∆FCD (chứng minh trên)
Suy ra: ˆC1 = ˆD1 (hai góc tương ứng)
Suy ra: DE // BC (vì có hai góc so le trong bằng nhau)
ΔΔBDC = ∆FCD => BC = DF (hai cạnh tương ứng)
Mà DE = 1 : 2 . DF(gt). Vậy DE = 1 : 2 . BC











