Question

Cho mặt phẳng (Q) và điểm M nằm ngoài mặt phẳng (Q).

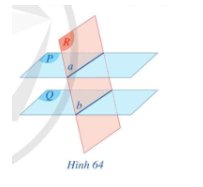
a) Trong mặt phẳng (Q) vẽ hai đường thẳng a’, b’ cắt nhau. Qua điểm M kẻ các đường thẳng a, và b lần lượt song song với a’, b’. Gọi (P) là mặt phẳng xác định bởi hai đường thẳng (cắt nhau) a và b (Hình 63). Mặt phẳng (P) có song song với mặt phẳng (Q) hay không?

b) Xét mặt phẳng (R) đi qua điểm M và song song với mặt phẳng (Q). Hai mặt phẳng (R) và (P) có trùng nhau hay không?

Answer 1

a) Ta có: a // a’ mà a’ ⊂ (Q) nên a // (Q);

               b // b’ mà b’ ⊂ (Q) nên b // (Q).

Do a // (Q);

      b // (Q);

      a, b cắt nhau tại M và cùng nằm trong mặt phẳng (P)

Suy ra (P) // (Q).

b) Do (R) // (Q) nên trong mp(R) tồn tại hai đường thẳng a’’, b’’ đi qua M và lần lượt song song với a’, b’ trong mp(Q).

Ta có: a // a’, a’’ // a’ nên a // a’’.

Mà a’’ ∈ (R), do đó a // (R)

Do hai mặt phẳng (P) và (R) có một điểm chung nên chúng có đường thẳng chung d.

Ta có:  a // (R);

            a ⊂ (P);

           (P) ∩ (R) = d.

Suy ra a // d.

Mà a, d cùng nằm trong mặt phẳng (P) và cùng đi qua điểm M nên đường thẳng a chính là giao tuyến của hai mặt phẳng (P) và (R).

Chứng minh tương tự ta cũng có đường thằng b cũng là giao tuyến của hai mặt phẳng (P) và (R).

Như vậy, hai mặt phẳng (P) và (R) có hai giao tuyến a và b nên (P) và (R) là hai mặt phẳng trùng nhau.