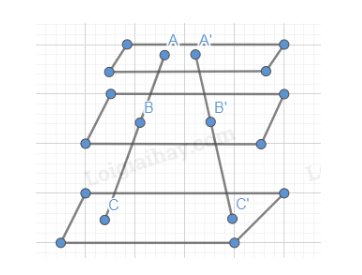
a) Ta có: AD // BC (ABCD là hình bình hành)
Mà AD thuộc (AFD), BC thuộc (BEC)
Nên (AFD) // (BEC)
b) Trong (ABEF) kẻ đường thẳng d qua M // AF
Ta có: d cắt AB tại I, d cắt EF tại J (1)
Trong (ABCD) có I thuộc (P) mà (P) // (AFD)
Suy ra từ I kẻ IH // AD (2)
(1)(2) suy ra (IJH) trùng (P) và // (AFD)
Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD)
Suy ra: IH cắt AC tại N
Ta có các hình bình hành IBCH, IBEJ
Gọi O là trung điểm của AB
Có M là trọng tâm △ABE
Suy ra: \(\dfrac{MO}{ME}=\dfrac{1}{2}\).
Ta có: AB // CD suy ra: AI // CH
Định lí Ta-lét: \(\dfrac{AN}{NC}=\dfrac{AI}{CH}\)
mà CH = IB (IBCH là hình bình hành)
Suy ra: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}\)
Ta có: AB // EF nên OI // EJ
Do đó: \(\dfrac{OI}{EJ}=\dfrac{MO}{ME}=\dfrac{1}{2}\)
Mà EJ = IB (IBEJ là hình bình hành)
Suy ra: \(\dfrac{OI}{IB}=\dfrac{1}{2}\) hay IB = 2OI
Ta có: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}=\dfrac{AO+OI}{2OI}\)
Mà OA = OB (O là trung điểm AB)
Nên \(\dfrac{AN}{NC}=2\).