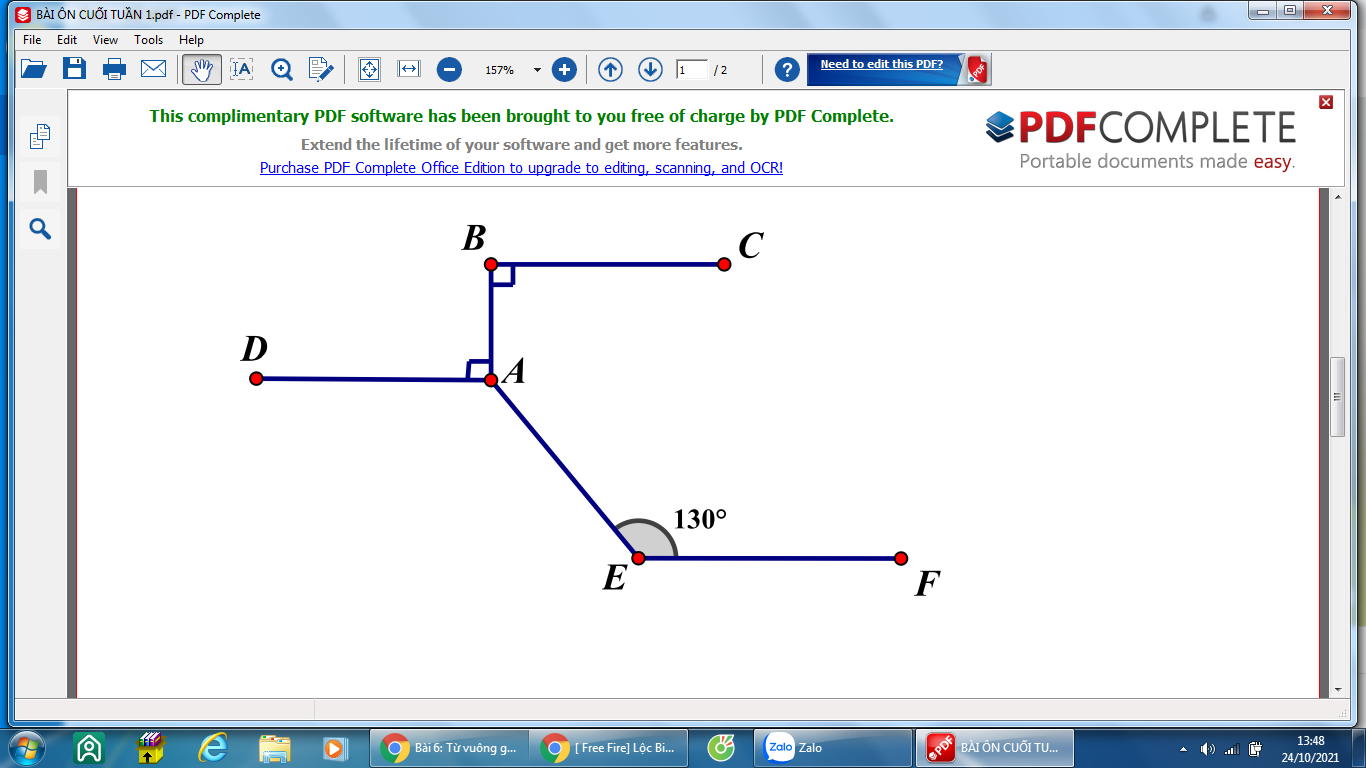
Kẻ At // BC
Suy ra: DE // At (vì cùng song song với BC)
Ta có : \(\widehat{CBA}\)=\(\widehat{BAt}\) ( Vì hai góc so le trong và BC // At)
=> \(\widehat{BAt}\) = \(20^0\) (1)
Lại có : \(\widehat{tAD}=\widehat{ADE}\) ( Vì hai góc so le trong và DE // At)
=> \(\widehat{tAD}=30^0\) (2)
Từ (1) và (2) suy ra:
\(\widehat{BAD}=\widehat{BAt}+\widehat{tAD}\)
= \(20^0+30^0=50^0\)
Vậy \(\widehat{BAD}=50^0\)
Giải:
Qua A dựng AG\(//\)BC (1)
Biết BC\(//\)DE (2)
Từ (1) và (2) \(\Rightarrow\) AG\(//\)BC\(//\)DE
Ta có: AG\(//\)BC
\(\widehat{A_1}=\widehat{B_1}=20^0\) ( Sole trong )
Ta lại có: AG\(//\)DE
\(\widehat{A_2}=\widehat{D_2}=30^0\) ( Sole trong )
\(\Rightarrow\widehat{BAD}=\widehat{A_1}+\widehat{A_2}\)
Thay số: \(\widehat{BAD}=20^0+30^0=50^0\)