Giải :
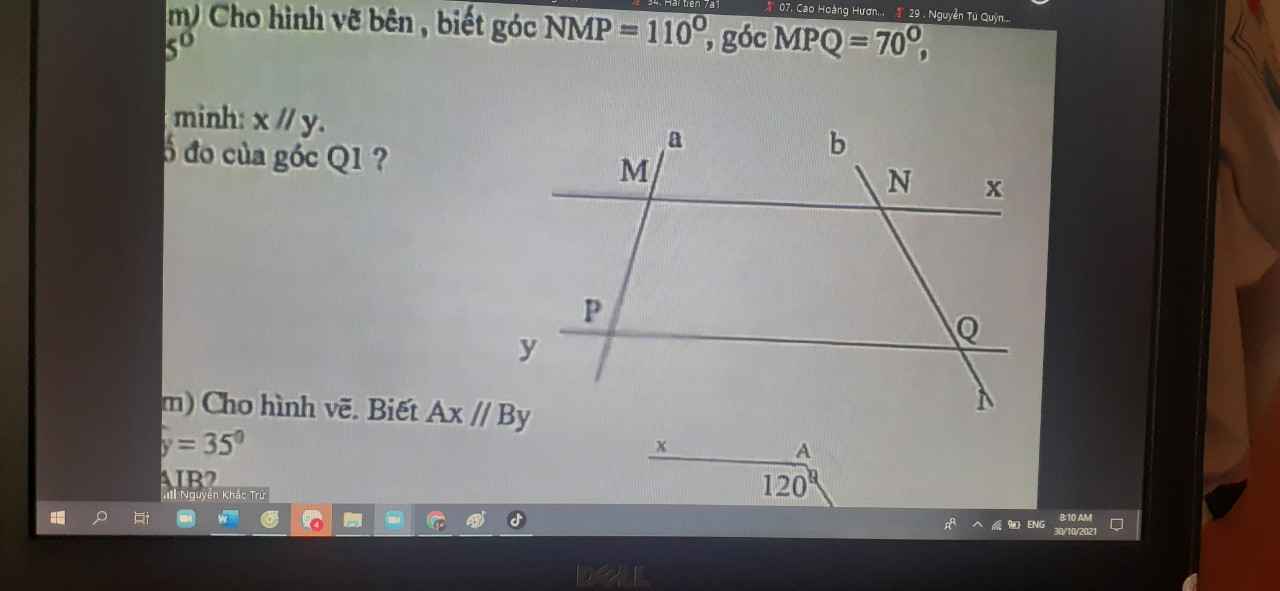
cánh 1: ta có : \(\widehat{A_3}\) + \(\widehat{A_4}\) = \(180^0\) ( 2 góc kề bù )
thay vào ta có : \(130^0\) + \(\widehat{A_4}\) = \(180^0\)
=> \(\widehat{A_4}\) = \(180^0\) - \(130^0\)
=> \(\widehat{A_4}\) = \(50^0\) = \(\widehat{B_2}\) ( so le trong )
Vậy a // b ( đpcm )
cánh 2: ta có: \(\widehat{A_3}\) đối đỉnh với \(\widehat{A_1}\)
=> \(\widehat{A_3}\) = \(\widehat{A_1}\) = \(130^0\)
=> \(\widehat{A_1}\) + \(\widehat{B_2}\) = \(130^0\) + \(50^0\) = \(180^0\)
=> 2 góc trong cùng phía bù nhau
vậy a // b .
Ta có hình vẽ:
\(\widehat{A3}=\widehat{A1}=130^o\)( đối đỉnh)
Mà \(\widehat{A1}+\widehat{B2}=130^o+50^o=180^o\)(2 góc trong cùng phía)
Nên:\(a//b\)
\(\Rightarrowđpcm\)
Ta có:
\(\widehat{B3}+\widehat{B2}=180^o\)(kề bù)
\(\Rightarrow\widehat{B3}+50^o=180^o\Rightarrow\widehat{B3}=130^o\)
Vì \(\widehat{A1}=\widehat{B3}=130^o\)(so le trong) nên \(a//b\)
\(\Rightarrowđpcm\)
Ta có:
\(\widehat{A3}=\widehat{B3}=180^o\)(đồng vị) nên \(a//b\)
\(\Rightarrowđpcm\)
C1: Ta có: \(\widehat{B_2}+\widehat{B_3}=180^0\) (kề bù)
\(Hay:50^0+\widehat{B_3}=180^0\)
\(\Rightarrow\widehat{B_3}=180^0-50^0=130^0\)
Vì \(\widehat{A_3}=\widehat{B_3}=130^0\)
Mà \(\widehat{A_3}\) và \(\widehat{B_3}\) ở vị trí đồng vị \(\Rightarrow a//b\)
C2: Có: \(\widehat{A_3}=\widehat{A_1}=130^0\) (hai góc đối đỉnh)
Vì \(\widehat{A_1}=\widehat{B_3}=130^0\) (theo cm ở C1)
Mà \(\widehat{A_1}\) và \(\widehat{B_3}\) ở vị trí đối đỉnh \(\Rightarrow a//b\)
C3: Ta có: \(\widehat{A_3}+\widehat{A_4}=180^0\) (kề bù)
\(Hay:130^0+\widehat{A_4}=180^0\)
\(\Rightarrow\widehat{A_4}=180^0-130^0=50^0\)
Do đó: \(\widehat{A_4}+\widehat{B_3}=50^0+130^0=180^0\) (theo cm C1)
Mà \(\widehat{A_4}\) và \(\widehat{B_3}\) ở vị trí trong cùng phía \(\Rightarrow a//b\)
Chúc bn hok tốt!![]()