Question

Cho hình thang \(ABCD\left( {AB//CD} \right)\) có \(AB = 6m,CD = 15m,OD = 8m\) (Hình 13). Tính độ dài đoạn thẳng \(OB\).

Answer 1

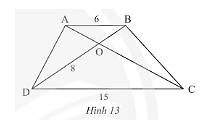
Vì tứ giác \(ABCD\) là hình thang có \(AB//CD\) nên \(\widehat {BAO} = \widehat {OCD}\) (hai góc so le trong)

Xét tam giác \(ABO\) và tam giác \(CDO\) có:

\(\widehat {BAO} = \widehat {OCD}\) (chứng minh trên)

\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)

Do đó, \(\Delta ABO\backsim\Delta CDO\) (g.g)

Ta có: \(\frac{{AB}}{{CD}} = \frac{{OB}}{{OD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Thay số, \(\frac{6}{{15}} = \frac{{OB}}{8} \Rightarrow OB = \frac{{6.8}}{{15}} = 3,2\)

Vậy \(OB = 3,2m\).