Xét ΔDAC có IM//AC
nên DM/DA=DI/DC
=>DI/DC=BN/BC
=>NI//BD
Đúng 0
Bình luận (0)
Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
Cho hình thang ABCD(AB//CD,AB<CD) lấy điểm M trên cạnh AD và điểm N trên cạnh BC sao cho \(\frac{DM}{DA}\)=\(\frac{BN}{BC}\) . Lấy điểm I trên cạnh CD sao cho MI // AC . Chứng minh IN // BD
Cho hình thang ABCD (đáyAB, CD; AB<CD) .Lấy điểm Mtrêncạnh AD và điểm N trên cạnh BC sao cho\(\frac{DA}{DA}=\frac{BN}{BC}\) .Lấy điểm I trên cạnh CD sao cho MI / / AC. MN cắt BD và AC tại E vàF.AC cắt BD tại O, IM cắt DO tại K, IN cắt CO tại H.Chứng minh: a)I N/ / BD b)ME=NF
Cho hình thang ABCD có AB// CD và AB < CD. Gọi E là giao điểm của AC ,BC biết AB = 2 cm, BC = 8 cm trên cạnh AD lấy điểm K sao cho AK = 1 cm, AD = 5 cm Chứng minh KO//DC
Câu 1: Cho hình thang ABCD (AB // CD) gọi I là giao điểm của hai đường chéo AC và BD. Một điểm M trên đấy AB và MA = 2cm, MB = 6cm, cạnh đáy CD = 12cm. Đường thẳng IM cắt đáy CD tại N. a) Tính tỉ số NC/ND b) Tính độ dài đoạn thẳng NC và ND
Cho hình thang ABCD (AB //CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q chứng minh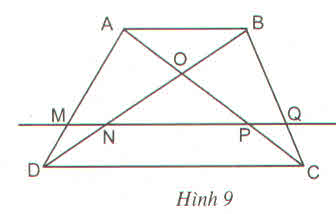 
DN\BD=CP\AC
Cho tam giác ABC có điểm M trên cạnh BC sao cho BC=4CM. Trên cạnh AC lấy điểm N sao cho CN/AN=1/3. Chứng minh MN // với AB
24 tháng 1 2022 lúc 20:07
Cho hình thang ABCD có hai đấy là AB và CD, M là trung điểm của AB, O là giao điểm của AD và BC. OM cắt CD tại N. Chứng minh N là trung điểm của CD
22 tháng 1 2021 lúc 11:41
Cho tứ giác ABCD có \(\widehat{A}=90^o;\widehat{D}=90^o\) . Góc A và góc D là hai góc đáy . Trên BC lấy điểm M là điểm nằm giữa sao cho MC=CD , MB= AB . Gọi giao điểm của AC và BD là N chứng minh MN\(\perp AD\)
Cho tam giác ABC có AB = 9cm, AC = 12cm. Trên cạnh AB lấy điểm H và trên cạnh AC lấy điểm K sao cho AH = 6cm, AK=8cm
a/ Chứng minh: HK // BC
b/ Cho biết BC = 18cm. Tính HK
c, Gọi M là trung điểm BC , AM cắt HK tại I . Chứng minh I là trunng điểm của HK
nêu rõ cách giải
BT1: Cho tam giác ABC, trung tuyến AM.Lấy điểm N trên cạnh AB, điểm Q trên cạnh AC sao cho NQ// BC. Gọi K là giao của AM và NQ. Cmr: NK=KQ.
BT2: Cho hình bình hành ABCD, trên tia đối của tia CB lấy điểm I, AI cắt BD,
DC lần lượt ở K,G. Chứng minh:
a, CI/IB=IG/AT
b, DG/DC=DK/KB
c, AK.BI = KI.AD
d, AK2= KG.KI