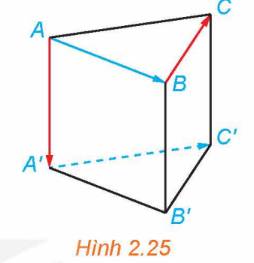
Vì ABC.A’B’C’ là lăng trụ tam giác đều nên AA’B’B là hình chữ nhật. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \). Do đó: \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {BB'} ,\overrightarrow {BC} } \right) = \widehat {B'BC} = {90^0}\) (do BB’C’C là hình chữ nhật)
Vì AA’B’B là hình chữ nhật nên \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right) = \widehat {C'A'B'}\).
Vì tam giác A’B’C’ là tam giác đều nên \(\widehat {C'A'B'} = {60^0}\). Do đó, \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = {60^0}\).