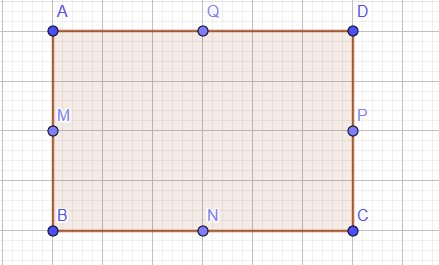
Áp dụng định lý Pytago: `QM = sqrt(AQ^2 + AM^2) = sqrt(((AB)/2)^2 + ((AD)/2)^2).`
`MN = sqrt(BM^2 + NB^2) = sqrt(((AB)/2)^2 + ((BC)/2)^2) = sqrt(((AB)/2)^2 + ((AD)/2)^2)`.
Chứng minh tương tự cho `NP, QP` ta thấy `QM = MN = NP = QP`.
Vậy tứ giác MNPQ là hình thoi.
Vì ABCD là hình chữ nhật nên AB = CD; AD = BC
Vì M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD. DA nên:
AQ = BN = CN = DQ
AM = BM = CP = DP
Xét 4 tam giác AQM, BNM, CNP. DQP có:
AQ = BN = CN = DQ
AM = BM = CP = DP
Suy ra:
\(\begin{array}{l}\Delta AQM = \Delta BNM = \Delta CNP = \Delta DQP\\ \Rightarrow QM = MN = NP = QP\end{array}\)
Vậy tứ giác MNPQ có QM = MN = NP = QP nên tứ giác MNPQ là hình thoi.





