Bài 4: Hai mặt phẳng vuông góc
Các câu hỏi tương tự
Cho hình chóp Sabcd có sa vuông góc với abcd , đáy abcd là hình chữ nhật có cạnh ab=a, ad=2a , sa= 2a căn 3
Gọi I là trung điểm của ab , mặt phẳng P qua I và vuông góc với Sb . Tính góc giữa mặt phẳng Sb và mp abcd
Giups mìnhhh với các bạn ơii , mk cần lời giải chi tiết , cảm ơnn nhiềuuu ah
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn thẳng SO
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD)
Cho hình chóp S.ABCD có độ dài cạnh đáy là a. Gọi O là giao điểm của AC và BD.Độ dài các cạnh bên là asqrt{2}. Măt phẳng mp(P) là mặt phẳng đi qua BD và vuông góc với SC. Tính Cotg của góc tạo bởi đường thẳng AB và mpleft(Pright) là bao nhiêu ? P/s: Trường THPT Phan Huy Chú ,thành phố Hà NộiEm xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạEm cám ơn nhiều lắm ạ!
Đọc tiếp
Cho hình chóp \(S.ABCD\) có độ dài cạnh đáy là \(a\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Độ dài các cạnh bên là \(a\sqrt{2}\). Măt phẳng mp(P) là mặt phẳng đi qua \(BD\) và vuông góc với \(SC\). Tính \(Cotg\) của góc tạo bởi đường thẳng \(AB\) và \(mp\left(P\right)\) là bao nhiêu ?
P/s: Trường THPT Phan Huy Chú ,thành phố Hà Nội
Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạ
Em cám ơn nhiều lắm ạ!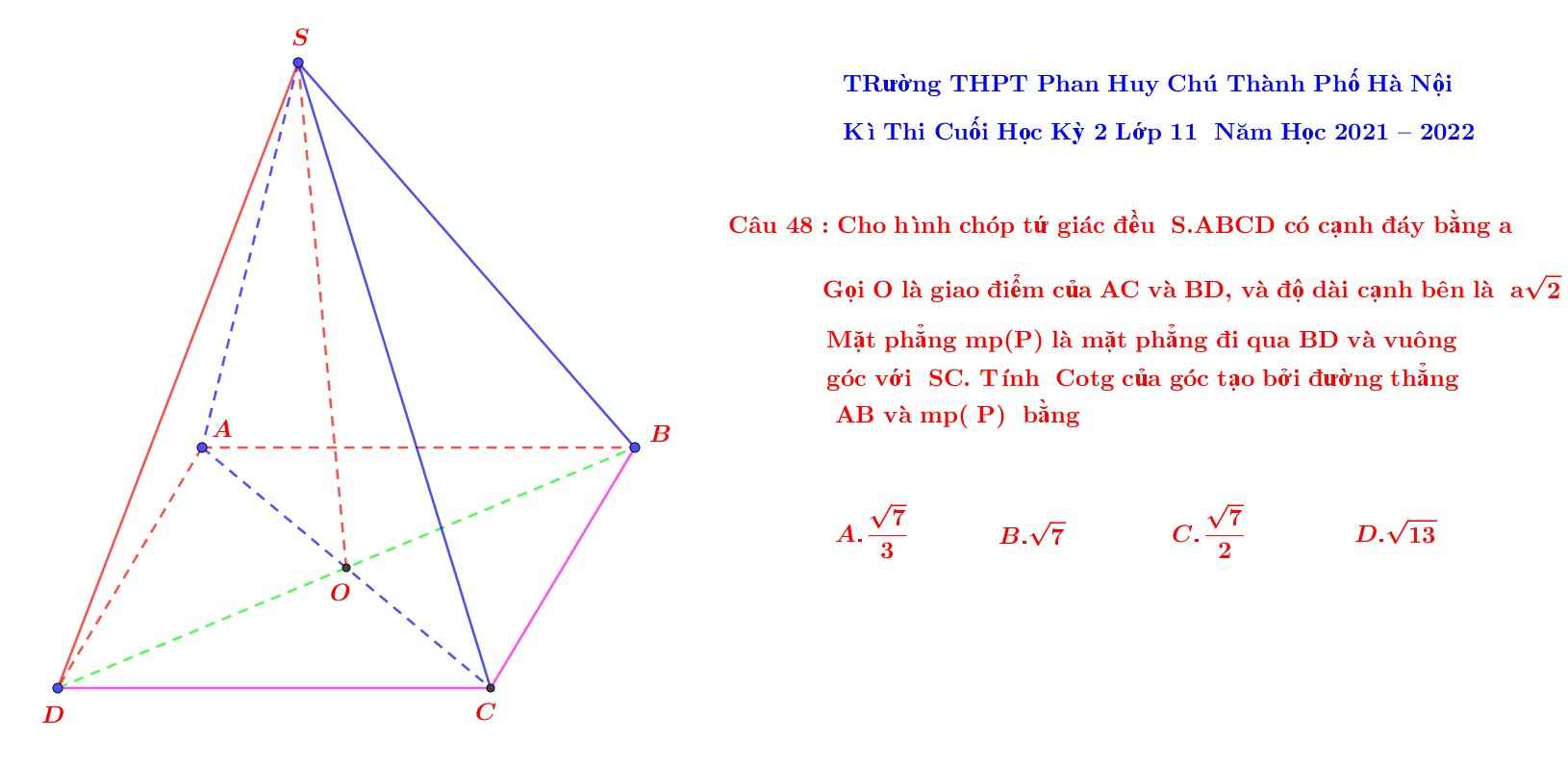
cho hình chóp S ABCD có đáy ABCD là hình thang vuông tại A và D với AB=2a, AD=DC=a, SA vuông góc với mặt phẳng ABCD, SA=a, E là trung điểm của AB
tính góc giữa (SCD) và (SBD)
giúp em voii ạ em cảm ơn nhìu!!!
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử left(alpharight) là mặt phẳng đi qua A và vuông góc với cạnh SC, left(alpharight) cắt SC tại I
a) Xác định giao điểm K của SO với phẳng left(alpharight)
b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // left(alpharight)
c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng left(alpharight). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng left(alpharight)
Đọc tiếp
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử \(\left(\alpha\right)\) là mặt phẳng đi qua A và vuông góc với cạnh SC, \(\left(\alpha\right)\) cắt SC tại I
a) Xác định giao điểm K của SO với phẳng \(\left(\alpha\right)\)
b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // \(\left(\alpha\right)\)
c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng \(\left(\alpha\right)\). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng \(\left(\alpha\right)\)
Cho hình chóp S.ABC, đáy là tam giác vuông tại C. Tam giác SAC là tam giác đều cạnh a nằm trong mặt phẳng vuông góc với đáy, cạnh AB bằng a căn 3. Gọi H là trung điểm AC. Chứng minh: a. (SBC) vuông góc (SAC) b. Tính góc giữa (SAB) và (ABC)
Cho hình chóp tứ giác đều S.ABCD , cạnh đáy bằng a , cạnh bên bằng \(\dfrac{a\sqrt{5}}{2}\). H là giao điểm AC và BD.
a) chứng minh: \(\left(SAC\right)\perp\left(SBD\right)\)
b) tính khoảng cách giữa 2 đường thẳng AC và SB
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.a) Tính độ dài đoạn SO.b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).d) gọi H là trung điểm CD. tính diện tích SCDcác bạn làm câu D thôi nha
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn SO.
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).
d) gọi H là trung điểm CD. tính diện tích SCD
các bạn làm câu D thôi nha
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và SA=SB=SC=a. Chứng minh rằng :
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD)
b) Tam giác SBD là tam giác vuông









