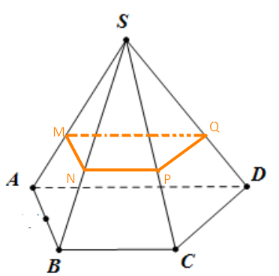
Xét tam giác SAD có: \(\dfrac{MA}{MS}=\dfrac{QD}{QS}\) suy ra MQ // AD do đó MQ // (ABCD)
Tương tự ta có: QP // (ABCD)
Vậy mp(MPQ) // mp(ABCD).
Lập luận tương tự, ta có mp(NPQ) // (ABCD).
Hai mặt phẳng (MPQ) và (NPQ) cùng đi qua điểm P và cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng đó trùng nhau, tức bốn điểm M, N, P, Q đồng phẳng.