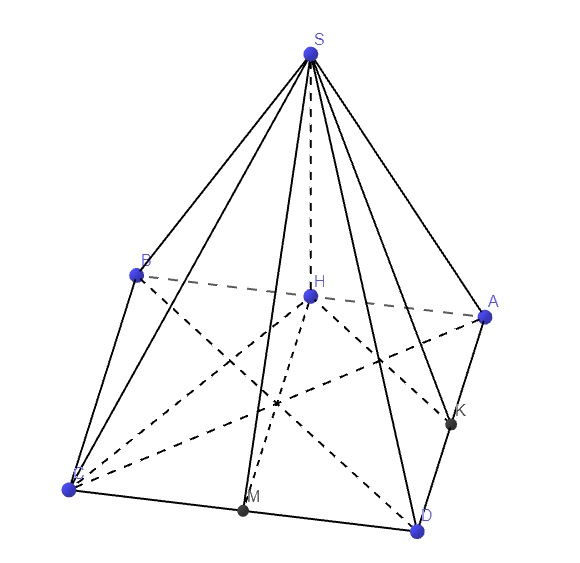
a.
Do tam giác SAB đều \(\Rightarrow SB=AB=a\)
Trong tam giác SBC ta có:
\(SB^2+BC^2=2a^2=SC^2\)
\(\Rightarrow\Delta SBC\) vuông tại B (pitago đảo)
\(\Rightarrow BC\perp SB\)
Mà \(BC\perp AB\left(gt\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
Do \(SH\in\left(SAB\right)\Rightarrow BC\perp SH\) (1)
Lại có SAB là tam giác đều, mà SH là đường trung tuyến (H là trung điểm AB)
\(\Rightarrow SH\) đồng thời là đường cao hay \(SH\perp AB\) (2)
(1);(2) \(\Rightarrow SH\perp\left(ABCD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow\) HM là hình chiếu vuông góc của SM lên (ABCD)
\(\Rightarrow\widehat{SMH}\) là góc giữa SM và (ABCD) hay \(\alpha=\widehat{SMH}\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(HM=BC=a\) \(\Rightarrow tan\alpha=\dfrac{SH}{HM}=\dfrac{\sqrt{3}}{2}\)
c.
Do H là trung điểm AB, K là trung điểm AD \(\Rightarrow\) HK là đường trung bình tam giác ABD
\(\Rightarrow HK||BD\)
Mà \(BD\perp AC\) (hai đường chéo hình vuông)
\(\Rightarrow HK\perp AC\) (3)
Lại có \(SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\) (4)
(3);(4) \(\Rightarrow AC\perp\left(SHK\right)\Rightarrow AC\perp SK\)