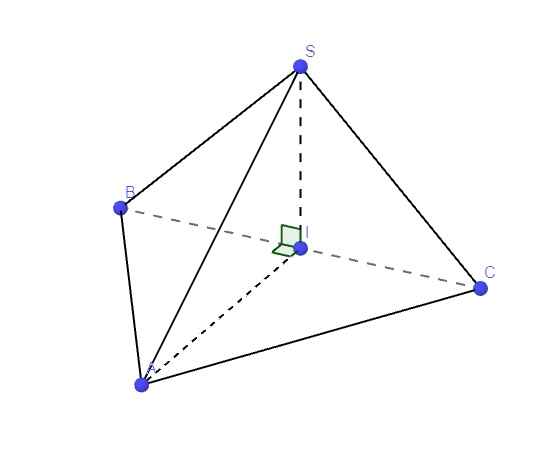
a.
Do ABC đều \(\Rightarrow\) AI là trung tuyến đồng thời là đường cao
\(\Rightarrow AI\perp BC\) (1)
SBC vuông cân tại S \(\Rightarrow SI\) là trung tuyến kiêm đường cao
\(\Rightarrow SI\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAI\right)\Rightarrow BC\perp SA\)
b.
\(SA>AI\Rightarrow\widehat{SIA}>\widehat{ASI}\Rightarrow\widehat{ASI}\) là góc nhọn
Do ABC đều \(\Rightarrow AI=\dfrac{a\sqrt{3}}{2}\)
SBC vuông cân tại S \(\Rightarrow SI=\dfrac{1}{2}BC=\dfrac{a}{2}\)
Áp dụng định lý hàm sin cho tam giác SAI:
\(\dfrac{SI}{sin\widehat{IAS}}=\dfrac{AI}{sin\widehat{ASI}}\Rightarrow sin\widehat{ASI}=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{ASI}=60^0\) (do \(\widehat{ASI}\) nhọn)
\(\Rightarrow=180^0-\left(30^0+60^0\right)=90^0\)
Hay \(SI\perp IA\)