Question

Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA \( \bot \) (ABC). Gọi M là trung điểm của BC. Chứng minh rằng:

a) BC \( \bot \) (SAM);

b) Tam giác SBC cân tại S.

Answer 1

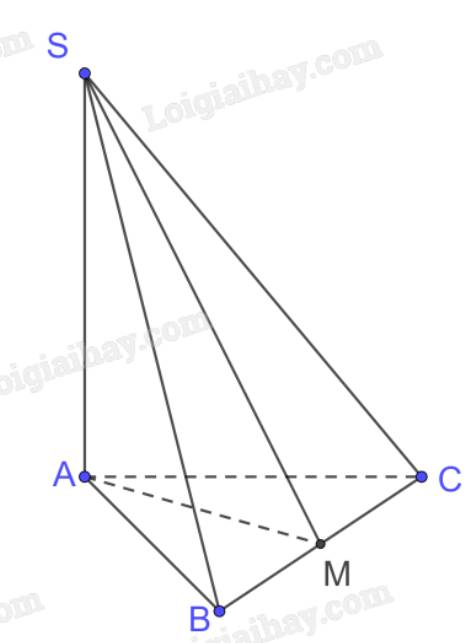
a) Xét tam giác ABC cân tại A có

AM là đường trung tuyến (M là trung điểm BC)

\( \Rightarrow \) AM là đường cao \( \Rightarrow \) \(AM \bot BC\)

Ta có:

 \(\left. \begin{array}{l}AM \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AM \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAM} \right)\)

b) \(\left. \begin{array}{l}BC \bot \left( {SAM} \right)\\SM \subset \left( {SAM} \right)\end{array} \right\} \Rightarrow BC \bot SM\)

Xét tam giác SBC có:

+) SM là đường cao \(\left( {BC \bot SM} \right)\)

+) SM là đường trung tuyến (M là trung điểm BC)

\( \Rightarrow \) Tam giác SBC cân tại S.