Hình như sai đề phải là MD = EP mới đúng bạn ạ, nếu không thì mdpe thì nó vần là hình bình hành MNPQ thôi:
Ta có:
Vì MD = EP mà MD // EP (vì trong hình bình hành MNPQ có MN // PQ)
=> Hình MDPE là hình bình hành
Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2 AB.
a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?
b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.
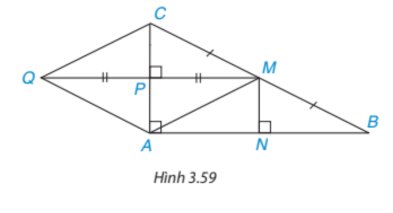
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.59)
a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau
b) Chứng minh tứ giác APMN là một hình chữ nhật. Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC
c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh rằng tứ giác AMCQ là một hình thoi
d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.
b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.
d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành.
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.
b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.
c) Tứ giác có ba góc vuông là hình chữ nhật.
d) Tứ giác có ba cạnh bằng nhau là hình thoi
Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân
Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N là chân đường vuông góc hạ từ B xuống ME (H.3.60)
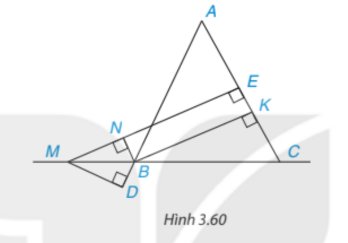
Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật
b) BK và NE cùng bằng hiệu khoảng cách từ M đến AC và AB (dù M thay đổi trên đường thẳng MC miễn là B nằm giữa M và C)
