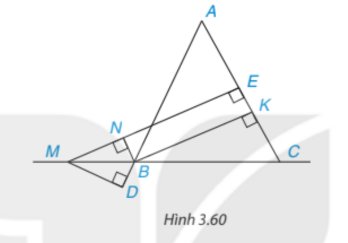
a) Xét tứ giác BPCD ta có: BP // CD, BP = CD (cùng bằng AB) suy ra BPCD là hình bình hành
b) ABD vuông cân tại A suy ra AB = AD, do đó ABCD là hình vuông
Khi đó BD là phân giác \(\widehat {ABC} \Rightarrow \widehat {DBC} = {45^o} \Rightarrow \widehat {DBP} = {45^o} + {90^o} = {135^o}\)
\(\widehat {PC{\rm{D}}} = \widehat {DBP} = {135^o}\)
BD//PC⇒\(\widehat {BPC} = \widehat {AB{\rm{D}}} = {45^o}\) (hai góc đồng vị)
\(\widehat {B{\rm{D}}C} = \widehat {BPC} = {45^o}\)