- ΔCNM ~ ΔCAB (vì MN // AB) (1)
- ΔMPB ~ ΔCAB (vì MP // AC) (2)
- Từ (1) và (2) => ΔCNM ~ ΔMPB
- ΔCNM ~ ΔCAB (vì MN // AB) (1)
- ΔMPB ~ ΔCAB (vì MP // AC) (2)
- Từ (1) và (2) => ΔCNM ~ ΔMPB
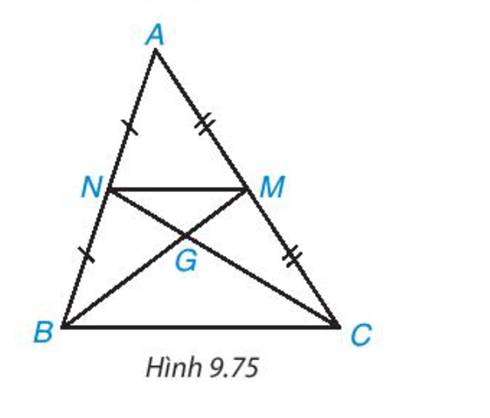
Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng.
Cho tam giác ABC có đường cao AH. Biết AH=12cm, CH=9cm, BH=16cm. Lấy M, N lần lượt là trung điểm của AH, BH
a) Chứng minh rằng ABC là tam giác vuông tại A
b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN
c) Tính diện tích tam giác AMN
Cho hình 9.74, biết rằng \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\). Chứng minh rằng ΔABD ∽ ΔACE và ΔBOE ∽ ΔCOD
Cho ΔA′B′C′ ∽ ΔABC với tỉ số đồng dạng bằng 2. Khẳng định nào sau đây là đúng:
A. \(\frac{{AB}}{{A'B'}} = 2\)
B. \(\frac{{AB}}{{A'C'}} = 2\)
C. \(\frac{{A'B'}}{{AB}} = 2\)
D. \(\frac{{A'B'}}{{AC}} = 2\)
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
a) \(\frac{{B{\rm{D}}}}{{BC}} = \frac{{AB}}{{AB + AC}}\), từ đó suy ra \(A{\rm{E}} = \frac{{AB.AC}}{{AB + AC}}\)
b) ΔDFC ∽ ΔABC
c) DF=DB
Cho tam giác ABC vuông tại A có AB=5cm, AC=4cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB
a) Chứng minh rằng ΔHDA ∽ ΔAHC
b) Tính độ dài các đoạn thẳng HA, HB, HC, HD
Trong các bộ ba số đo dưới đây, đâu là số đo ba cạnh của một tam giác vuông?
A. 3 m; 5 m; 6 m
B. 6 m; 8 m; 10 m
C. 1 cm; 0,5 cm; 1,25 cm
D. 9 m; 16 m; 25 m.
Cho ABC là tam giác không cân. Biết ΔA′B′C′ ∽ ΔABC. Khẳng định nào sau đây là đúng?
A. ΔA′C′B′ ∽ ΔACB
B. ΔB′C′A′ ∽ ΔBAC
C. ΔB′A′C′ ∽ ΔBCA
D. ΔA′C′B′ ∽ ΔABC
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều nào dưới đây không suy ra ΔABC ∽ ΔDEF
A. \(\widehat B = \widehat E\)
B. \(\widehat C = \widehat F\)
C. \(\widehat B + \widehat C = \widehat E + \widehat F\)
D. \(\widehat B - \widehat C = \widehat E - \widehat F\)