Bài tập cuối chương 9

Hướng dẫn giải

Khẳng định A là khẳng định đúng 

(Trả lời bởi Mai Trung Hải Phong)

Hướng dẫn giải

- Có ΔA′B′C′ ∽ ΔABC

=> \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 2\)

=> Đáp án đúng là đáp án C

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Xét đáp án B nhận thấy: \({6^2} + {8^2} = {10^2}\)

⇒ Đáp án đúng là đáp án B

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Đáp án đúng là đáp án C.

Vì \(\widehat B + \widehat C = \widehat E + \widehat F\) chưa thể suy ra được \( \widehat B = \widehat E\) và \( \widehat C = \widehat F \)

(Trả lời bởi Hà Quang Minh)

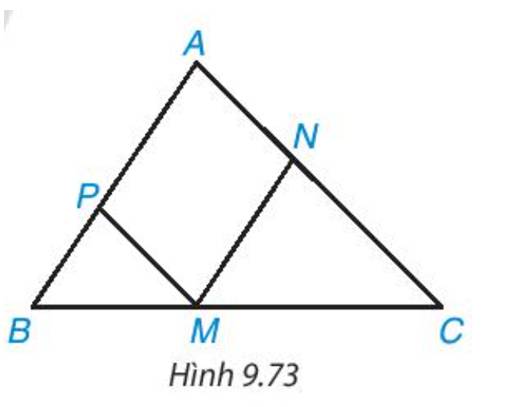
Hướng dẫn giải

-  ΔCNM ~ ΔCAB (vì MN // AB) (1)

- ΔMPB ~ ΔCAB (vì MP // AC) (2)

- Từ (1) và (2) => ΔCNM ~ ΔMPB 

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

- Xét tam giác ABD và tam giác ACE có \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\), góc A chung

=> ΔABD ∽ ΔACE (g.g)

- Vì ΔABD ∽ ΔACE 

=> \(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}C}\)

=> \(\widehat {C{\rm{D}}O} = \widehat {BEO}\) (1)

- Có \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\)

Mà \(\widehat {AB{\rm{D}}} + \widehat {EBO} = {180^o}\)

      \(\widehat {AC{\rm{E}}} + \widehat {DCO} = {180^o}\)

=> \(\widehat {EBO} = \widehat {DCO}\) (2)

Từ (1) và (2) => ΔBOE ∽ ΔCOD (g.g)

(Trả lời bởi Hà Quang Minh)

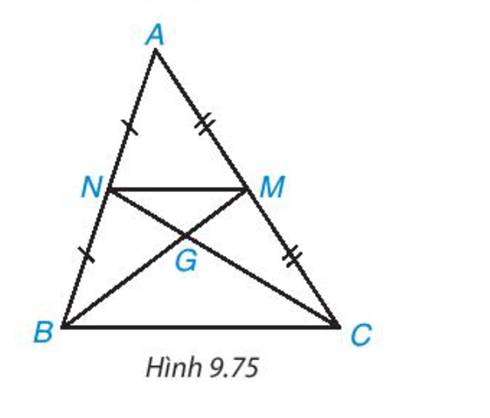
Hướng dẫn giải

- Xét tam giác ABC có, NA=NB, MA=MC

=> NM là đường trung bình của tam giác ABC

=> NM // BC, \(NM = \frac{1}{2}AB\)

- Xét tam giác GMN và tam giác GBC có NM // BC => ΔGMN ∽ ΔGBC 

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

a) Có AB ⊥ AC, HD ⊥ AB

=> HD // AC

=> \(\widehat {DHA} = \widehat {HAC}\)

- Xét tam giác vuông HDA (vuông tại D) và tam giác vuông AHC (vuông tại H) có: \(\widehat {DHA} = \widehat {HAC}\)

=> ΔHDA ∽ ΔAHC 

b) Xét tam giác ABC có: \(A{B^2} + A{C^2} = B{C^2}\)

mà AB=5cm, AC=4cm

=> \(BC = \sqrt {41} \)

- Có AH.BC=AB.AC

=> \(AH = \frac{{20\sqrt {41} }}{{41}}\)

=> \(H{B^2} = A{B^2} - A{H^2}\) (áp dụng định lý Pythagore trong tam giác vuông BHA)

=> \(HB = \frac{{25\sqrt {41} }}{{41}}\)

=> \(HC = \frac{{16\sqrt {41} }}{{41}}\)

- Xét tam giác vuông BDH và tam giác vuông BAC có: HD // AC

=> ΔBDH ∽ ΔBAC 

=> \(\frac{{BH}}{{BC}} = \frac{{DH}}{{AC}}\)

=> \(H{\rm{D}} = \frac{{100}}{{41}}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

a) Xét tam giác AHB vuông tại H, có:

\(A{H^2} + H{B^2} = A{B^2}\) (định lý Pythagore)

=> \(A{B^2} = {12^2} + {16^2}\)

=> AB=20cm

Tương tự, có: \(A{C^2} = A{H^2} + C{H^2}\) (áp dụng định lý Pythagore trong tam giác vuông AHC)

=> \(A{C^2} = {12^2} + {9^2}\)

=> AC=15cm

Có BC=9+16=25

Trong tam giác ABC, nhận thấy \(A{B^2} + A{C^2} = B{C^2}\)

=> Tam giác ABC vuông tại A

b) Xét tam giác AHB có: 

M là trung điểm của AH

B là trung điểm của BH

=> MN là đường trung bình của tam giác AHB

=> MN // AB

mà AB ⊥ AC (vì tam giác ABC vuông tại A)

=> MN ⊥ AC

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

a) Vì AD là tia phân giác của góc BAC \( \Rightarrow \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} \Rightarrow DB.AC = DC.AB(*)\)

Ta có: \(B{\rm{D}}.\left( {AB + AC} \right) = B{\rm{D}}.AB + B{\rm{D}}.AC = DB.AB + DC.AB + AB.\left( {DB + DC} \right) = AB.BC\)

\(\begin{array}{l} \Rightarrow B{\rm{D}}.\left( {AB + AC} \right) = AB.BC\\ \Rightarrow \frac{{B{\rm{D}}}}{{BC}} = \frac{{AB}}{{AB + AC}}(1)\end{array}\)

\(\Delta CE{\rm{D}} \backsim \Delta CAB\left( {{{\widehat C}^{}}chung{;^{}}\widehat A = \widehat E} \right)\)

\(\begin{array}{l} \Rightarrow \frac{{CE}}{{CA}} = \frac{{C{\rm{D}}}}{{CB}}\\ \Rightarrow \frac{{AC - A{\rm{E}}}}{{AC}} = \frac{{BC - B{\rm{D}}}}{{BC}} \Rightarrow 1 - \frac{{A{\rm{E}}}}{{AC}} = 1 - \frac{{DB}}{{BC}}\\ \Rightarrow \frac{{A{\rm{E}}}}{{AC}} = \frac{{DB}}{{BC}}(2)\end{array}\)

Từ (1), (2) suy ra: \(\frac{{A{\rm{E}}}}{{AC}} = \frac{{AB}}{{AB + AC}} \Rightarrow A{\rm{E}} = \frac{{AB.AC}}{{AB + AC}}\)

b) \(\begin{array}{l}\Delta DFC \backsim \Delta ABC\\ \Rightarrow \frac{{DF}}{{AB}} = \frac{{DC}}{{AC}} \Rightarrow DF = \frac{{AB.DC}}{{AC}}(3)\end{array}\)

Từ (*) ta có: \(DB = \frac{{DC.AB}}{{AC}}(4)\)

Từ (3), (4) suy ra: DF = DB

(Trả lời bởi Hà Quang Minh)