SGK Chân trời sáng tạo - Tập 1 - Trang 19
18 tháng 8 lúc 14:05
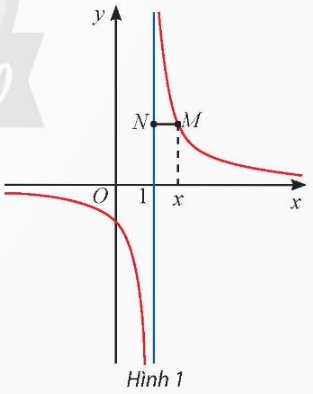
Cho hàm số \(y=\dfrac{1}{x-1}\) có đồ thị như Hình 1.
a) Tìm \(\lim\limits_{x\rightarrow1^+}\dfrac{1}{x-1},\lim\limits_{x\rightarrow1^-}\dfrac{1}{x-1}\).
b) Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi x → 1+; x → 1−.
