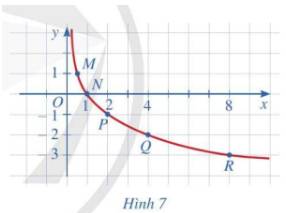
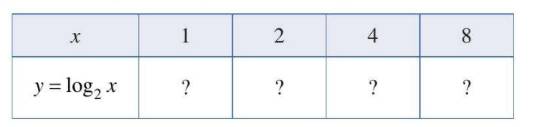
Cho hàm số mũ \(y = {2^x}\)
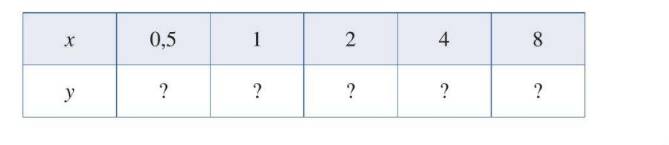
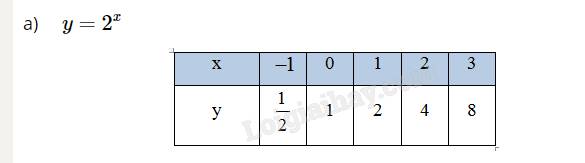
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
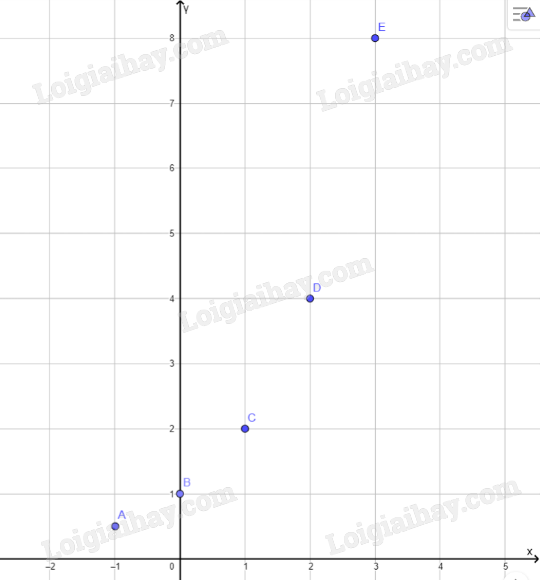
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.
Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {2^x}\) (Hình 1)
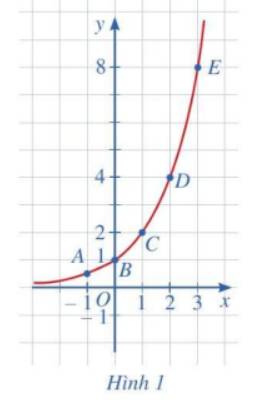
c) Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {2^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.
d) Quan sát đồ thị hàm số \(y = {2^x}\), nêu nhận xét về:
\(\mathop {\lim {2^x}}\limits_{x \to + \infty } ;\,\mathop {\lim {2^x}}\limits_{x \to - \infty } \)Sự biến thiên của hàm số \(y = {2^x}\) và lập bảng biến thiên của hàm số đó.a:
| x | -1 | 0 | 1 | 2 | 3 |
| y | \(\dfrac{1}{2}\) | 1 | 2 | 4 | 8 |
b: Tham khảo:
c: Tọa độ giao điểm của hàm số với trục tung là B(0;1)
Đồ thị hàm số này ko cắt trục hoành
d:
\(\lim\limits_{x\rightarrow+\infty}2^x=+\infty;\lim\limits_{x\rightarrow-\infty}2^x=+\infty\)
=>Hàm số này đồng biến trên R
Bảng biến thiên:

tham khảo
b) Biểu diễn các điểm ở câu a: