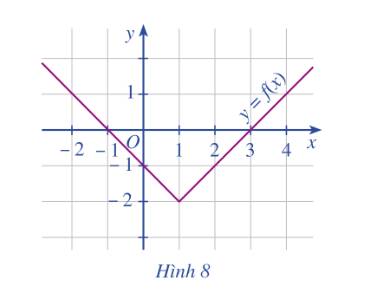
a) Ta có:
\(f\left( 1 \right) = 1 + 1 = 2\)
\(f\left( 2 \right) = 2 + 1 = 3\)
\( \Rightarrow f\left( 2 \right) > f\left( 1 \right)\)
b) Ta có:
\(f\left( {{x_1}} \right) = {x_1} + 1;f\left( {{x_2}} \right) = {x_2} + 1\)
\(\begin{array}{l}f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \left( {{x_1} + 1} \right) - \left( {{x_2} + 1} \right)\\ = {x_1} - {x_2} < 0\end{array}\)
Vậy \({x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).