Question

Cho hai đường thẳng phân biệt ∆₁, ∆₂ lần lượt đi qua các điểm M₁, M₂ và tương ứng có vectơ chỉ phương là \(\overrightarrow{u_1},\overrightarrow{u_2}\).

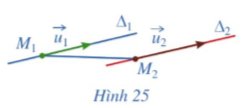
a) Giả sử ∆₁ song song với ∆₂ (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow{u_1}\) và \(\overrightarrow{u_2}\); \(\overrightarrow{u_1}\) và \(\overrightarrow{M_1M_2}\)?

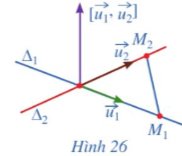
b) Giả sử ∆₁ và ∆₂ cắt nhau (Hình 26). Hai vectơ \(\overrightarrow{u_1}\) và \(\overrightarrow{u_2}\) có cùng phương hay không? Ba vectơ \(\overrightarrow{u_1},\overrightarrow{u_2}\) và \(\overrightarrow{M_1M_2}\) có đồng phẳng hay không?

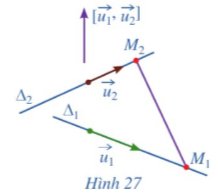
c) Giả sử ∆₁ và ∆₂ chéo nhau (Hình 27). Hai vectơ \(\overrightarrow{u_1}\) và \(\overrightarrow{u_2}\) có cùng phương hay không? Ba vectơ \(\overrightarrow{u_1},\overrightarrow{u_2}\) và \(\overrightarrow{M_1M_2}\) có đồng phẳng hay không?

Answer 1

a) Vì \({\Delta _1}\) song song với \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.

Vì \({M_1}\) thuộc đường thẳng \({\Delta _1}\), \({M_2}\) thuộc đường thẳng \({\Delta _2}\)  nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \) không cùng phương.

b) Vì \({\Delta _1}\) và \({\Delta _2}\) cắt nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) đồng phẳng.

c) Vì \({\Delta _1}\) và \({\Delta _2}\) chéo nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) không đồng phẳng.