Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
Các câu hỏi tương tự
6 vị trí tương đối của các cặp đường thẳng sau : a d1 : 14x+y+20 và d2 : x+4y+10+10 b d1 : d2: c d1 : d2 : 2x+4y-100 d d1 : x+y-20 và d2: 2x+y-30 7 Viết phương trình đường thẳng d đi qua M( 2;5) và cách đều hai điểm A(-1;2) , B(5;4) 8 Tìm trên đường thẳng ΔΔ : x-y+20 điểm M cách đều hai điểm E(0;4) , F(4;-9)9 Cho đường thẳng d: x-y0 và điểm M (2;1) a Viết phương trình đường thẳng đối xứng với d qua điểm M b Tìm hình chiếu của điểm M trên D .
Đọc tiếp
6> vị trí tương đối của các cặp đường thẳng sau :
a> d1 : 14x+y+2=0 và d2 : x+4y+10+1=0
b> d1 : 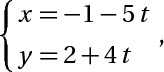 d2:
d2: 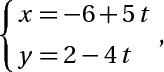
c> d1 : 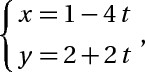 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0
d> d1 : x+y-2=0 và d2: 2x+y-3=0
7> Viết phương trình đường thẳng d đi qua M( 2;5) và cách đều hai điểm A(-1;2) , B(5;4)
8 Tìm trên đường thẳng ΔΔ : x-y+2=0 điểm M cách đều hai điểm E(0;4) , F(4;-9)
9> Cho đường thẳng d: x-y=0 và điểm M (2;1)
a> Viết phương trình đường thẳng đối xứng với d qua điểm M
b> Tìm hình chiếu của điểm M trên D .
cho đường thẳng (d) có phương trình tổng quát : 2x-y+3=0 và đi qua M(3,1) : a) viết phương trình đường thẳng (d') đi qua M và vuông góc với (d) ; b) tìm điểm H là giao điểm của (d) và (d') ; c) tìm M' là điểm đối xứng với M qua (d) .
cho đường thẳng (d) có phương trình tổng quát : 2x - y + 3 = 0 và đi qua M(3;1) : a) viết phương trình đường thẳng (d') đi qua M và vuông góc với (d) ; b) tìm điểm H là giao điểm của (d) và (d') ; c) tìm M' là điểm đối xứng với M qua (d) .
cho đường thẳng (d) có phương trình tổng quát : 2x-y+3=0 và đi qua M(3,1) : a) viết phương trình đường thẳng (d') đi qua M và vuông góc với (d) ; b) tìm điểm H là giao điểm của (d) và (d') ; c) tìm M' là điểm đối xứng với M qua (d) .
cho đường thẳng (d) có phương trình tổng quát : 2x - y + 3 = 0 và đi qua M(3;1) : a) viết phương trình đường thẳng (d') đi qua M và vuông góc với (d) ; b) tìm điểm H là giao điểm của (d) và (d') ; c) tìm M' là điểm đối xứng với M qua (d) .
cho đường thẳng (d) có phương trình tổng quát : 2x-y+3=0 và đi qua M(3,1) : a) viết phương trình đường thẳng (d') đi qua M và vuông góc với (d) ; b) tìm điểm H là giao điểm của (d) và (d') ; c) tìm M' là điểm đối xứng với M qua (d) .
cho đường thẳng d có phương trình x - y = 0 và điểm M(2;1) : a) viết phương trình tổng quát của đường thẳng đối xứng với đường thẳng d qua điểm M ; b) tìm hình chiếu của M trên đường thẳng d .
cho đường thẳng d có phương trình x - y = 0 và điểm M(2;1) : a) tìm hình chiếu của M trên đường thẳng d .
viết phương trình tổng quát của : a) đường thẳng Ox ; b) đường thẳng Oy ; c) đường thẳng đi qua M (x0,y0) và song song với Ox ; d) đường thẳng M (x0,y0) và vuông góc với Ox ; e) đường thẳng OM , với M (x0,y0) khác điểm O .



