Cho hai đường thẳng ∆1, ∆2 trong không gian có vectơ chỉ phương lần lượt là \(\overrightarrow{u_1},\overrightarrow{u_2}\). Giả sử ∆'1, ∆'2 là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với ∆1, ∆2 (Hình 28).
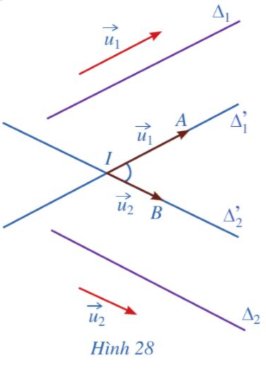
a) Nếu mối liên hệ giữa hai góc (∆1, ∆2) và (∆'1, ∆'2).
b) Gọi A và B là các điểm lần lượt thuộc hai đường thẳng ∆'1 và ∆'2 sao cho \(\overrightarrow{IA}=\overrightarrow{u_1},\overrightarrow{IB}=\overrightarrow{u_2}\). So sánh:
\(\cos\left(\Delta'_1,\Delta'_2\right),\left|\cos\left(\overrightarrow{IA},\overrightarrow{IB}\right)\right|,\left|\cos\left(\overrightarrow{u_1},\overrightarrow{u_2}\right)\right|\).
c) So sánh \(\cos\left(\Delta_1,\Delta_2\right)\) và \(\dfrac{\left|\overrightarrow{u_1}.\overrightarrow{u_2}\right|}{\left|\overrightarrow{u_1}\right|.\left|\overrightarrow{u_2}\right|}\).


