a) Ta thấy: số mũ của x trong hai đơn thức trên bằng nhau (đều bằng 2).
b) \(2{x^2} + 3{x^2} = {x^2} + {x^2} + {x^2} + {x^2} + {x^2} = 5{x^2}\) .
c) Ta có: \((2 + 3){x^2} = 5{x^2}\).
Vậy \(2{x^2} + 3{x^2}\) = \((2 + 3){x^2}\).
Cho đa thức \(P(x) = {x^2} + 2{x^2} + 6x + 2x - 3\).
a) Nêu các đơn thức của biến x có trong đa thức P(x).
b) Tìm số mũ của biến x trong từng đơn thức nói trên.
c) Thực hiện phép cộng các đơn thức có cùng số mũ của biến x sao cho trong đơn thức P(x) không còn hai đơn thức nào có cùng số mũ của biến x.
Cho đa thức \(R(x) = - 2{x^2} + 3{x^2} + 6x + 8{x^4} - 1\).
a) Thu gọn đa thức R(x).
b) Trong dạng thu gọn của đa thức R(x), sắp xếp các đơn thức theo số mũ giảm dần của biến.
Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.
a) \( - 2x\) b) \( - {x^2} - x + \dfrac{1}{2}\) ; c) \(\dfrac{4}{{{x^2} + 1}} + {x^2}\);
d) \({y^2} - \dfrac{3}{y} + 1\); e) \( - 6z + 8\); g) \( - 2{t^{2021}} + 3{t^{2020}} + t - 1\).
Trong giờ học môn Mĩ thuật, bạn Hạnh dán lên trang vở hai hình vuông có kích thước lần lượt là 3 cm và x cm như ở Hình 1. Tổng diện tích của hai hình vuông đó là \({x^2} + 9(c{m^2})\).
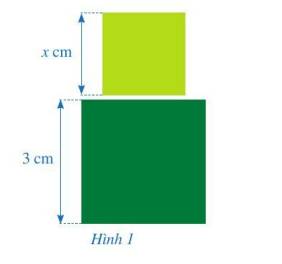
Biểu thức đại số \({x^2} + 9\)có gì đặc biệt?
Thực hiện mỗi phép tính sau:
a) \(\dfrac{4}{9}x + \dfrac{2}{3}x\); b) \( - 12{y^2} + 0,7{y^2}\); c) \( - 21{t^3} - 25{t^3}\).
Cho đa thức \(P(x) = 9{x^4} + 8{x^3} - 6{x^2} + x - 1 - 9{x^4}\).
a) Thu gọn đa thức P(x).
b) Tìm số mũ cao nhất của x trong dạng thu gọn của P(x).
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) x = 4 và x = – 4 là nghiệm của đa thức\(P(x) = {x^2} - 16\).
b) y = – 2 là nghiệm của đa thức \(Q(y) = - 2{y^3} + 4\).
a) Tính giá trị của biểu thức đại số \(3x - 2\) tại x = 2.
b) Tính giá trị của đa thức P(x) = \( - 4x + 6\) tại x = – 3.
Biểu thức nào sau đây là đa thức một biến?
a) \({x^2} + 9;\)
b) \(\dfrac{2}{{{x^2}}} + 2x + 1;\)
c) \(3x + \dfrac{2}{5}y.\)
