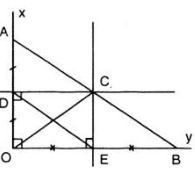
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, đường trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng :
a) CE = OD
b) \(CE\perp CD\)
c) CA = CB
d) CA // DE
e) Ba điểm A, B, C thẳng hàng
c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).
c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).
các bn ơi cx câu hỏi này các bn cm dùm mình: tam giác odc=tam giác ceo đi
a, Ta có Ox⊥Oy và CE ⊥ Oy
⇒ Ox song song CE (1)
- Ta cũng có: Oy ⊥ Ox
CD ⊥ Ox
⇒ Oy ⊥ CD (2)
Từ (1) và (2), ta có:
Ox song song CE và Oy song song CD
⇒ CE ≠ OD ( tính chất đoạn chắn) (đpcm)
b, Ta có Ox song song CE (do (1)), mà CD⊥ Ox
⇒ CD ⊥ CE (đpcm)
c, Vì C nằm trên đường trung trực của đoạn thẳng OA nên: CA= CO (3)
Vì C nằm trên đường trung trực của đoạn thẳng OB nên: CB=CO(4)
⇒ CA=CB (đpcm)
d, Xét 2 tam giác vuông DAC và CED, có:
CD cạnh chung
∠ADC=∠DCE= 90 độ
AD=CE (do OD = DA = CE)
Vậy ΔDAC = △CED ⇒ ∠ACD=∠EDC
Hơn nữa ∠ACD so le trong với ∠EDC⇒ CA song song DE (đpcm)
e, Tương tự câu d ta chứng minh được CB song song DE
Vậy ta được AC song song DE
CB song song DE
⇒ A, B, C thẳng hàng.