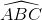 là góc tạo bởi hai tiếp tuyến BA và dây cung BC của (O). Dây BC = R suy ra
là góc tạo bởi hai tiếp tuyến BA và dây cung BC của (O). Dây BC = R suy ra![]() =
= 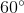 và
và 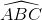 =
= 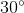 .
.
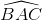 =
= 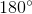 -
- 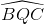 =
= 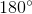 -
- 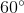 =
= 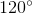 (tổng các góc của một tứ giác bằng
(tổng các góc của một tứ giác bằng 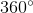 )
)

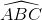 là góc tạo bởi hai tiếp tuyến BA và dây cung BC của (O). Dây BC = R suy ra
là góc tạo bởi hai tiếp tuyến BA và dây cung BC của (O). Dây BC = R suy ra![]() =
= 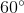 và
và 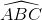 =
= 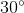 .
.
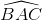 =
= 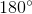 -
- 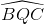 =
= 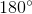 -
- 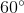 =
= 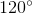 (tổng các góc của một tứ giác bằng
(tổng các góc của một tứ giác bằng 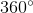 )
)
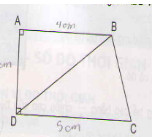
Cho đường tròn (O;R) và dây cung BC=R . Hai tiếp tuyến của đường tròn (O) tại B,C cắt nhau ở A . Tính góc ABC và góc BAC
Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Tính góc ABC và góc BAC
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến kẻ từ A đối với đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D. Chứng minh rằng \(\widehat{CBA}=\widehat{DBA}.\)
Cho nửa đường tròn (O,R) đường kính BC. Vẽ hai tiếp tuyến Bx và Cy (B,C là hai tiếp tuyến)Gọi A là điểm thuộc đường tròn sao cho cung AB nhỏ hơn cung AC, tiếp tuyến tại điểm A cắt Bx,Cy lần lượt tại D và E.
a)Cm:BD+CE=DE
b)Cm:góc DOE =90 độ và BD.CE=R mũ 2
c)CD cắt BE tại I.Vẽ AH vuông góc BC(H thuộc BC).Cm ba điểm A,I,H thẳng hàng
cho (O;R) và dây BC k qua tâm. Tiếp tuyến tại B và C của( O;R) cắt nhau tại a a) CM 4 điểm A,B,O,C cùng thuộc 1 đường tròn b) CM: OA vuông góc vs BC c) kẻ đường kính CD của (O) kẻ BH vuống góc vs CD. CMR BC là tai phân giác của góc ABH
. Cho đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. Trên tia đối của tia AB lấy điểm P, kẻ tiếp tuyến PT với đường tròn (O) và tiếp tuyến PE với đường tròn (O’) với T và E là hai tiếp điểm. Chứng mình rằng PTE PET
Cho tam giác ABC nội tiếp trong đường tròn (O). Vẽ tia Bx sao cho tia BC nằm giữa hai tia Bx; BA và \(\widehat{CBx}=\widehat{BAC}\).
Chứng minh rằng Bx là tiếp tuyến của (O) ?
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).