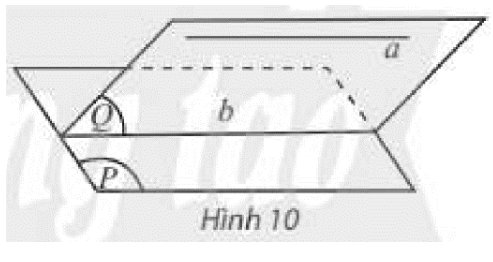
Hai đường thẳng a, b không có điểm chung.
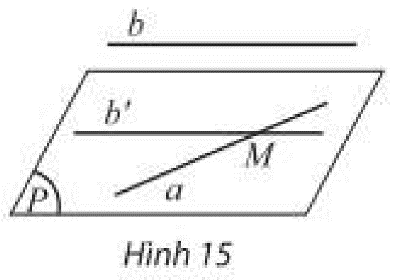
Cho đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và \(a\) song song với một đường thẳng \(b\) nằm trong \(\left( P \right)\). Đặt \(\left( Q \right) = mp\left( {a,b} \right)\).
a) Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
b) Giả sử \(a\) có điểm chung \(M\) với \(\left( P \right)\) thì điểm \(M\) phải nằm trên đường thẳng nào? Điều này có trái với giả thiết \(a\parallel b\) hay không?
Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha \right)\) với các cạnh \(AC,CD\) và \(DB\).
a) Chứng minh \(MNPQ\) là hình bình hành.
b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình bình hành có \(O\) là giao điểm hai đường chéo. Cho \(M\) là trung điểm của \(SC\).
a) Chứng minh đường thẳng \(OM\) song song với hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBA} \right)\);
b) Tìm giao tuyến của hai mặt phẳng \(\left( {OMD} \right)\) và \(\left( {SAD} \right)\).
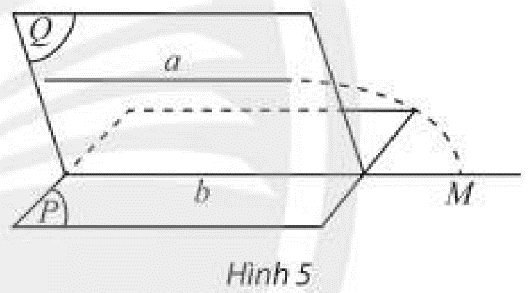
Cho hai đường thẳng chéo nhau \(a,b\). Lấy một điểm \(M\) trên \(a\), vẽ đường thẳng \(b'\) đi qua \(M\) và song song với \(b\). Đặt \(\left( P \right)\) là mặt phẳng đi qua \(a,b'\).
a) Có nhận xét gì về mối liên hệ giữa \(b\) và \(\left( P \right)\).
b) Gọi \(\left( {P'} \right)\) là mặt phẳng chứa \(a\) và song song với \(b\). Có nhận xét gì về mối liên hệ giữa \(b'\) và \(\left( {P'} \right)\); \(\left( P \right)\) và \(\left( {P'} \right)\)?
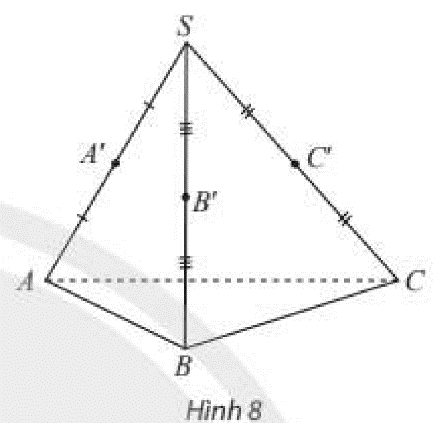
Cho hình chóp \(S.ABC\) có \(A',B',C'\) lần lượt là trung điểm của \(SA,SB,SC\). Tìm các đường thẳng lần lượt nằm trong, cắt, song song với mặt phẳng \(\left( {ABC} \right)\).
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không nằm trong cùng một mặt phẳng. Gọi \(O\) và \(O'\) lần lượt là tâm của \(ABCD\) và \(ABEF\).
a) Chứng minh đường thẳng \(OO'\) song song với các mặt phẳng \(\left( {CDF{\rm{E}}} \right),\left( {ADF} \right)\) và \(\left( {BCE} \right)\).
b) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AF\) và \(BE\). Chứng minh \(MN\parallel \left( {CDF{\rm{E}}} \right)\).
c) Tìm giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\).
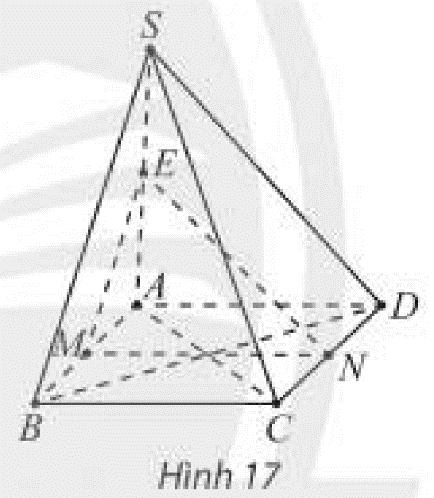
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M,N,E\) lần lượt là trung điểm của các đoạn thẳng \(AB,CD,SA\) (Hình 17). Chứng minh rằng:
a) \(MN\) song song với hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\);
b) \(SB\) và \(SC\) song song với mặt phẳng \(\left( {MNE} \right)\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, đáy lớn \(AB\). Gọi \(M\) là trung điểm của \(CD\), \(\left( P \right)\) là mặt phẳng qua \(M\) song song với \(SA\) và \(BC\). Tìm giao tuyến của \(\left( P \right)\) với các mặt của hình chóp \(S.ABCD\).
Cho hai hình bình hành \(ABCD\) và \(ABMN\) không đồng phẳng. Tìm số giao điểm của mặt phẳng \(\left( {ABCD} \right)\) lần lượt với các đường thẳng \(MN,MA\) và \(AC\).
