Chương II - Đường tròn
Các câu hỏi tương tự
cho đoạn thẳng ab trên cùng một nửa mặt phẳng ab vẽ hai tia ã, by cùng vuông góc với ab gọi o là trung điểm ab trên tia ã by lần lượt lấy hai điểm C và D bất kỳ sao cho COD = 90 chứng minh Cd là tiếp tuyến của hai đường tròn đường kính AB tìm vị trí của C D để diện tích tứ giác ABDC nhỏ nhất và tính diện tích ấy theo AB = a
Cho điểm C thuộc đoạn thẳng AB (C ≠ A, B). Trên cùng một nửa mặt phẳng bờ AB vẽ hai tia Ax, By vuông góc với AB. Trên tia Ax lấy một điểm I khác A, vẽ đường tròn đường kính IC. Tiếp tuyến tại C của đường tròn này cắt tia By tại K, IK cắt đường tròn tại P.a) Chứng minh 4 điểm C, P, K, B cùng thuộc một đường tròn.b) Chứng minh rằng: AI.BK AC.BC.c) Cho A, B, I cố định. Tìm vị trí điểm C để diện tích tứ giác ABKI đạt giá trị lớn nhất.
Đọc tiếp
Cho điểm C thuộc đoạn thẳng AB (C ≠ A, B). Trên cùng một nửa mặt phẳng bờ AB vẽ hai tia Ax, By vuông góc với AB. Trên tia Ax lấy một điểm I khác A, vẽ đường tròn đường kính IC. Tiếp tuyến tại C của đường tròn này cắt tia By tại K, IK cắt đường tròn tại P.a) Chứng minh 4 điểm C, P, K, B cùng thuộc một đường tròn.b) Chứng minh rằng: AI.BK = AC.BC.c) Cho A, B, I cố định. Tìm vị trí điểm C để diện tích tứ giác ABKI đạt giá trị lớn nhất.
cho nửa đường tròn tâm O đường kính AB,trên cùng 1 nửa mặt phẳng có bờ AB chứa nửa đường tròn vẽ các tiếp tuyến Ax;By.M và N lần lượt thuộc tia Ax và By sao cho góc MON=90°,gọi I là trung điểm của MN a)CMR:AB là tiếp tuyến của đường tròn(I;IO) b)CMR:MO là tia phân giác của góc AMN c)CMR:MN là tiếp tuyến của đường tròn(O;AB)
Cho đoạn thẳng AB và O là trung điểm của nó. Vẽ về một phía của AB các tia Ax, By cùng vuông góc với AB. Các điểm M, N theo thứ tự dịch chuyển trên Ax, By sao cho các góc MON bằng 90 độ. Gọi I là trung điểm của MN. AB là tiếp tuyến của đường tròn (I;IO), MO là tia phân giác của góc AMN. Cm:a) MN là tiếp tuyến của đường tròn đường kính ABb) Khi các điểm M, N thay đổi trên Ax, By thì AM. BN không đổic) Tìm vị trí của M để MA + BN nhỏ nhấtd) Xđ vị trí của điểm H (H là chân đường vuông góc hạ từ O x...
Đọc tiếp
Cho đoạn thẳng AB và O là trung điểm của nó. Vẽ về một phía của AB các tia Ax, By cùng vuông góc với AB. Các điểm M, N theo thứ tự dịch chuyển trên Ax, By sao cho các góc MON bằng 90 độ. Gọi I là trung điểm của MN. AB là tiếp tuyến của đường tròn (I;IO), MO là tia phân giác của góc AMN. Cm:
a) MN là tiếp tuyến của đường tròn đường kính AB
b) Khi các điểm M, N thay đổi trên Ax, By thì AM. BN không đổi
c) Tìm vị trí của M để MA + BN nhỏ nhất
d) Xđ vị trí của điểm H (H là chân đường vuông góc hạ từ O xuống MN) để diện tích tam giác AHB lớn nhất
Cho đoạn thẳng AB với trung điểm O. Trên nửa mặt phẳng bờ AB kẻ các tia Ax, By vuông góc vớiAB. Một góc vuông POQ quay xung quanh O cắt Ax, By tại P, Q. Gọi P’ là giao điểm của các tia đốicủa các tia OP, By.a) Tam giác QPP’ là tam giác gì, tại sao ?b) Chứng minh rằng đường thẳng PQ luôn luôn tiếp xúc với đường tròn (O,OA).c) Chứng minh rằng đường tròn ngoại tiếp OPQ luôn luôn tiếp xúc với một đường thẳng cố định
Đọc tiếp
Cho đoạn thẳng AB với trung điểm O. Trên nửa mặt phẳng bờ AB kẻ các tia Ax, By vuông góc với
AB. Một góc vuông POQ quay xung quanh O cắt Ax, By tại P, Q. Gọi P’ là giao điểm của các tia đối
của các tia OP, By.
a) Tam giác QPP’ là tam giác gì, tại sao ?
b) Chứng minh rằng đường thẳng PQ luôn luôn tiếp xúc với đường tròn (O,OA).
c) Chứng minh rằng đường tròn ngoại tiếp OPQ luôn luôn tiếp xúc với một đường thẳng cố định
Cho nửa đường tròn (O; R) đường kính AB. Trên cùng một mặt phẳng bờ AB chứa nửa đường tròn, kẻ hai tia tiếp tuyến Ax, By với nửa đường tròn. Lấy điểm M trên nửa đường tròn. Tiếp tuyến của nửa đường tròn tại M cắt Ax, By lần lượt tại C và D. chứng minh COD là tam giác vuông
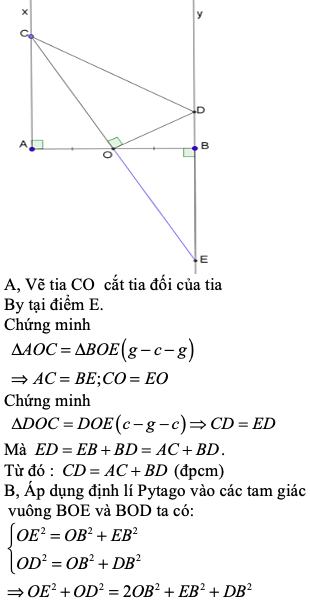
Cho đoạn thẳng AB, 2 đường thẳng d và d' lần lượt vuông góc với AB tại A và B. Gọi O là trung điểm của AB. Lấy C, D thuộc d và d' sao cho góc COD bằng 90 độ. Chứng minh CD là tiếp tuyến của đường tròn đường kính AB.
(Gợi ý: Vẽ OH vuông góc với CD, rồi tìm cách chứng minh OA = OH).
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.
a) AC cắt DO tại M, BC cắt OE tại N. Tử giác CMON là hình gì? Vì sao?
b) Chứng minh rằng MO.DM + ON.NE không đổi
c) AN cắt CO tại điểm H. Điểm H di chuyển trên đường nào khi C di chuyển trên nửa đường tròn (O; R).
Đọc tiếp
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E. a) AC cắt DO tại M, BC cắt OE tại N. Tử giác CMON là hình gì? Vì sao? b) Chứng minh rằng MO.DM + ON.NE không đổi c) AN cắt CO tại điểm H. Điểm H di chuyển trên đường nào khi C di chuyển trên nửa đường tròn (O; R).
Cho nửa đường tròn (O) đường kính AB. Trên cùng một nửa mặt phẳng bờ AB chứa nửa đường tròn vẽ hai tiếp tuyến Ax và By với (O). Lấy M bất kì trên (O). Kẻ tiếp tuyến thứ 3 với nửa đường tròn tại M cắt Ax và By tại C và D.1) CMR: Tam giác COD là tam giác vuông và tích AC.BD không phụ thuộc vào vị trí của M.2) AM cắt OC tại E, BM cắt OD tại F. Tứ giác MÈO là hình gì?3) Tứ giác AEFO; ADFB là hình gì?4)CMR: EC.EO + FO.FD R25) CMR: AB là tiếp tuyến của đường tròn ngoại tiếp tam giác COD.6) Xác định v...
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Trên cùng một nửa mặt phẳng bờ AB chứa nửa đường tròn vẽ hai tiếp tuyến Ax và By với (O). Lấy M bất kì trên (O). Kẻ tiếp tuyến thứ 3 với nửa đường tròn tại M cắt Ax và By tại C và D.
1) CMR: Tam giác COD là tam giác vuông và tích AC.BD không phụ thuộc vào vị trí của M.
2) AM cắt OC tại E, BM cắt OD tại F. Tứ giác MÈO là hình gì?
3) Tứ giác AEFO; ADFB là hình gì?
4)CMR: EC.EO + FO.FD = R2
5) CMR: AB là tiếp tuyến của đường tròn ngoại tiếp tam giác COD.
6) Xác định vị trí của M để chu vi; diện tích hình thang ACDB đạt giá trị nhỏ nhất.
7) Tia BM cắt Ax tại K. CMR: C là trung điểm AK.
8) Kẻ đường cao MH của tam giác AMB. MH cắt BC tại N; CMR: N là trung điểm MH và A, N, D thẳng hàng.