Cách làm của bạn là đúng rồi. Mình bổ sung một cách lí luận khác, dựa vào tính chất của hàm số bậc nhất: y = ax + b
Thì a là hệ số góc của đồ thì hàm số trên, \(a=\tan\alpha\)
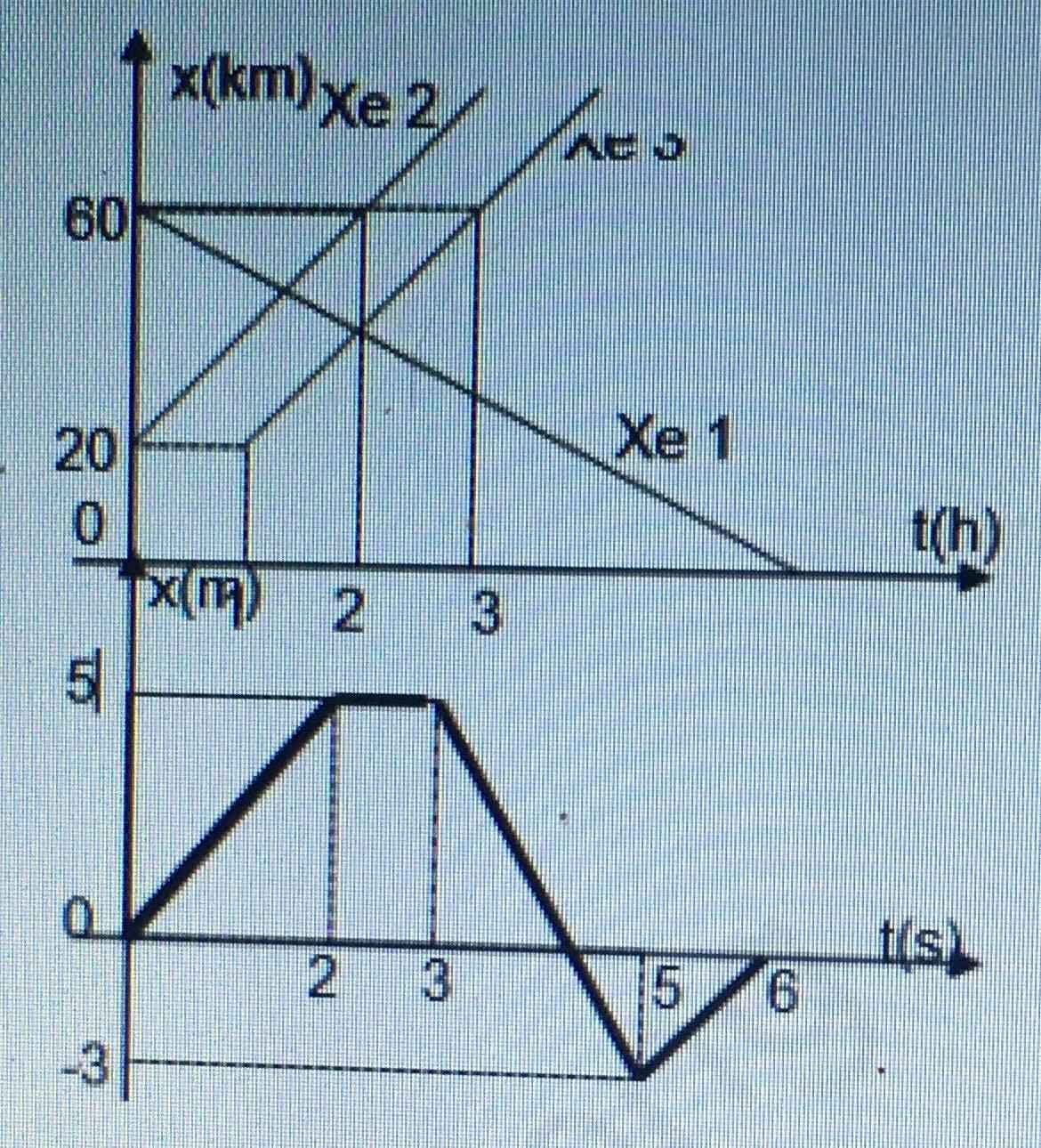
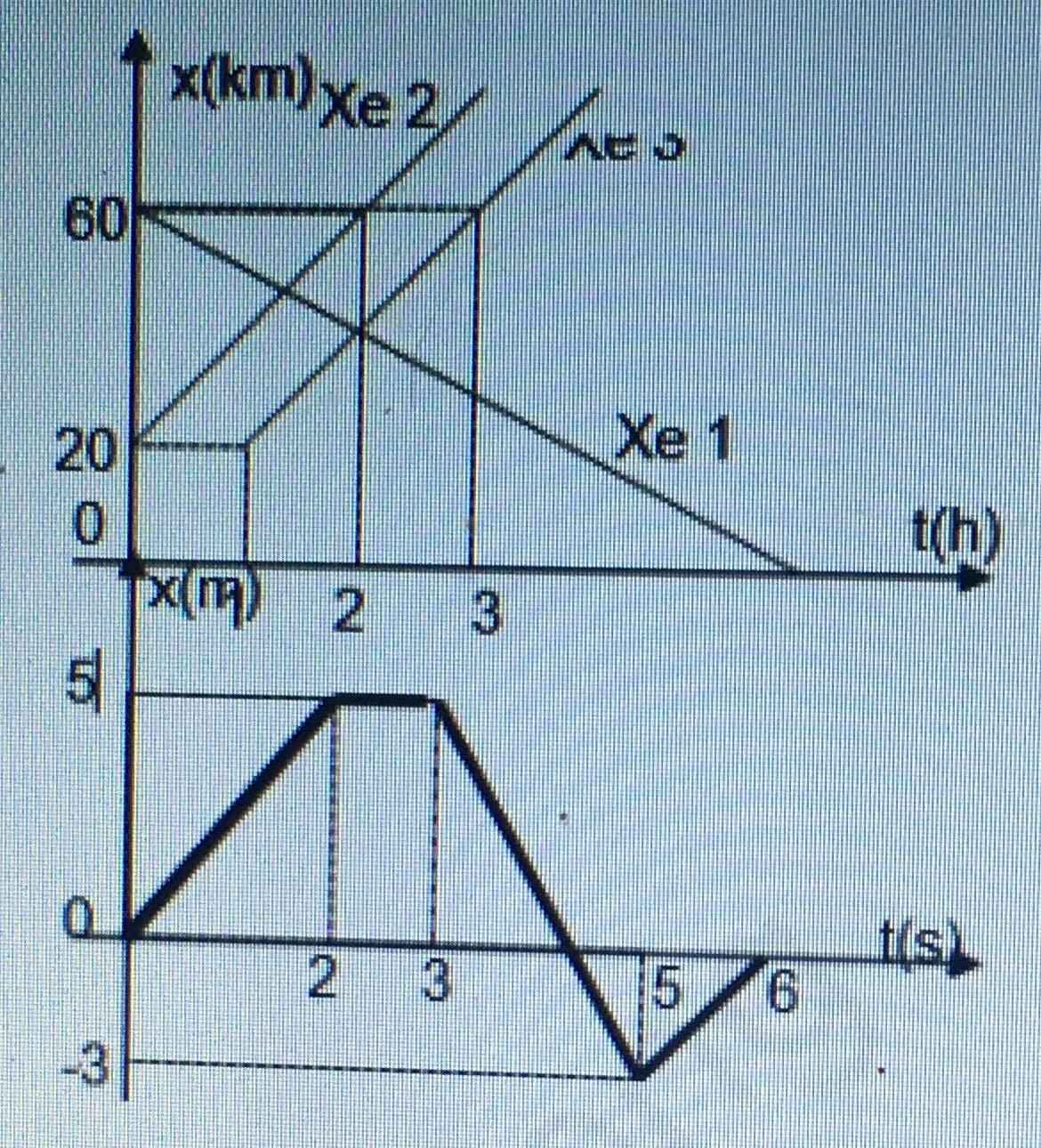
Do vậy ta có pt chuyển động tổng quát: \(x=x_0+v.t\)
+ Xe A: \(x_0=4\); \(v=\tan\alpha = \tan30^0=0,577\)
Suy ra pt chuyển động: \(x_A=4+0,577.t\) (m)
+ Xe B: \(x_0=0\); \(v=\tan\beta=\tan60^0=1,732\)
Suy ra ot chuyển động: \(x_B=1,732.t\) (m)
a) Hai xe chuyển động thẳng đều.
b) Theo đồ thị thì chuyển động của a, b đều là chuyển động cùng chiều dương của trục tọa độ. Chọn to là lúc vật bắt đầu chuyển động. Dạng phương trình cđ của hai xe là: x=xo+v(t).
xe a sẽ là: xa = xoa + va(t)
xe b sẽ là: xb = xob + vb(t)
Xét đồ thị của xe a. t=0 thì xa=4 => xa = 4+vat. (m) (1)
Từ điểm giao nhau trên đồ thị ta gọi tung độ là xt hoành độ là tx.
Thay vào pt 1 ta có: xt = 4 + vatx =>va = (xt-4)/tx
tan\(\alpha\)= tan 30 = (xt-4)/tx (Các bạn nhìn đồ thị xem đúng không). Từ đó => va= 0,577 (m/s)
pt xa = 4 + 0,577t.
Xét đồ thị của xe b t=0 thì x=0 => xo=0. ptcđ xb=vbt
Với điểm giao nhau trên đồ thị như ở trên ta có:
xt = vbtx => vb = xt/tx
Ta lại có tan 60 = xt/tx => vb = 1,732 (m/s)
pt xb = 1,732t.