Cho biết hai vectơ \(\overrightarrow{a}=\left(2;1;1\right),\overrightarrow{b}=\left(1;-2;0\right)\) có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong Hình 5. Tìm vectơ \(\overrightarrow{n}\) có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành ba đường thẳng đôi một vuông góc).
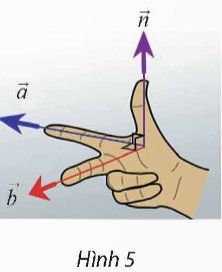
Theo hình vẽ, do vectơ \(\vec n\) có giá vuông góc lần lượt với giá của hai vectơ \(\vec a\) và \(\vec b\), nên có thể chọn vectơ \(\vec n\) là tích có hướng của hai vectơ \(\vec a\) và \(\vec b\).
Tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) là
\(\left[ {\vec a,\vec b} \right] = \left( {1.0 - 1.\left( { - 2} \right);1.1 - 2.0;2.\left( { - 2} \right) - 1.1} \right) = \left( {2;1; - 5} \right)\).
Do đó, vectơ \(\vec n\) cần tìm là \(\vec n = \left( {2;1; - 5} \right)\).


