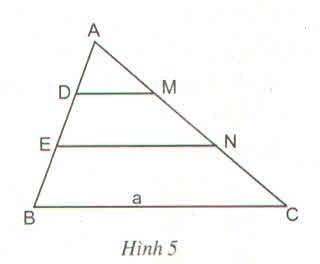
a) Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
\(\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}\)(t/c đường phân giác của tam giác)(1)
Xét ΔABC có
CE là đường phân giác ứng với cạnh AB(gt)
\(\Rightarrow\frac{AC}{BC}=\frac{AE}{EB}\)(t/c đường phân giác của tam giác)(2)
Ta có: ΔABC cân tại A(gt)
⇒AB=AC(3)
Từ (1), (2) và (3) suy ra
\(\frac{AE}{EB}=\frac{AC}{BC}=\frac{AD}{DC}\)
hay \(\frac{AE}{EB}=\frac{AD}{DC}\)
Xét ΔABC có \(\frac{AE}{EB}=\frac{AD}{DC}\)(cmt)
nên DE//BC(định lí talet đảo)(đpcm)