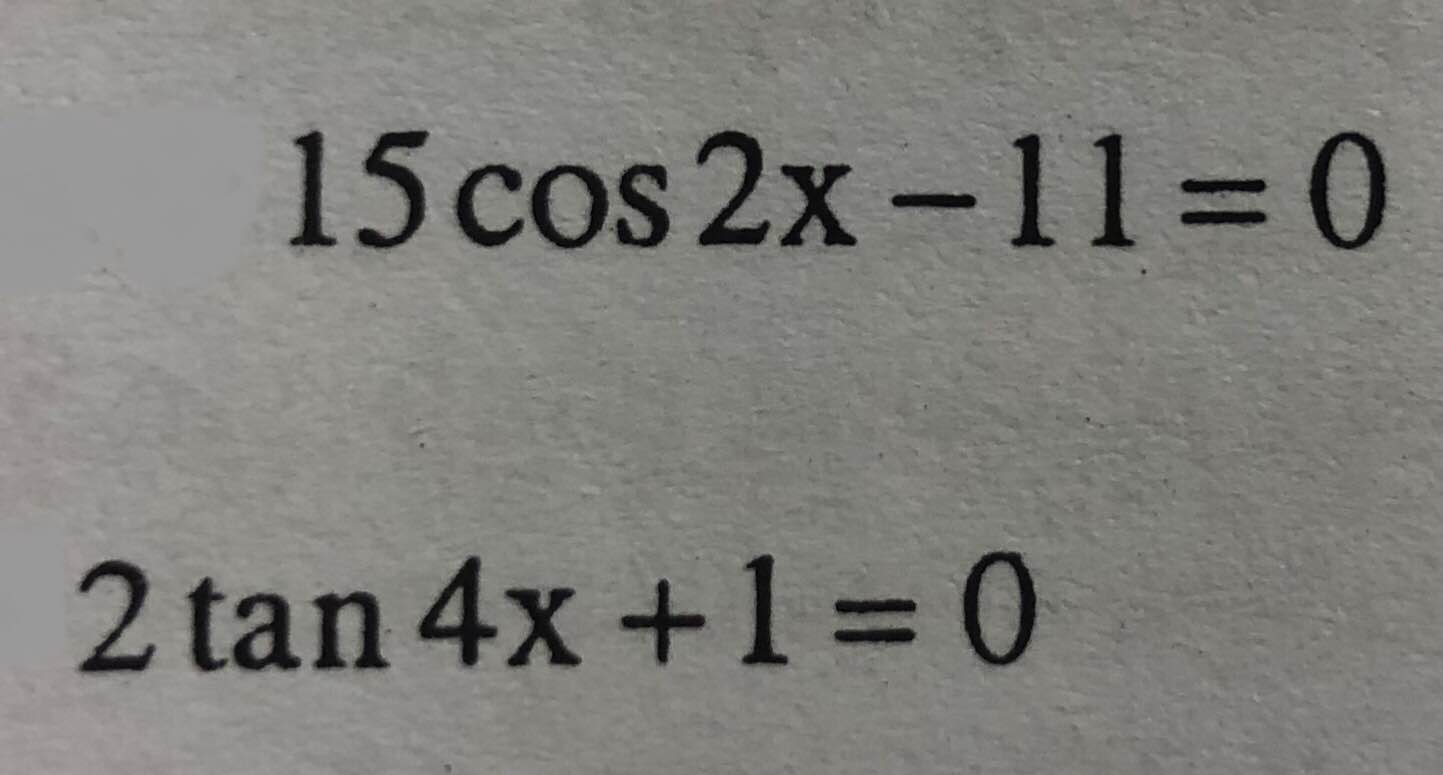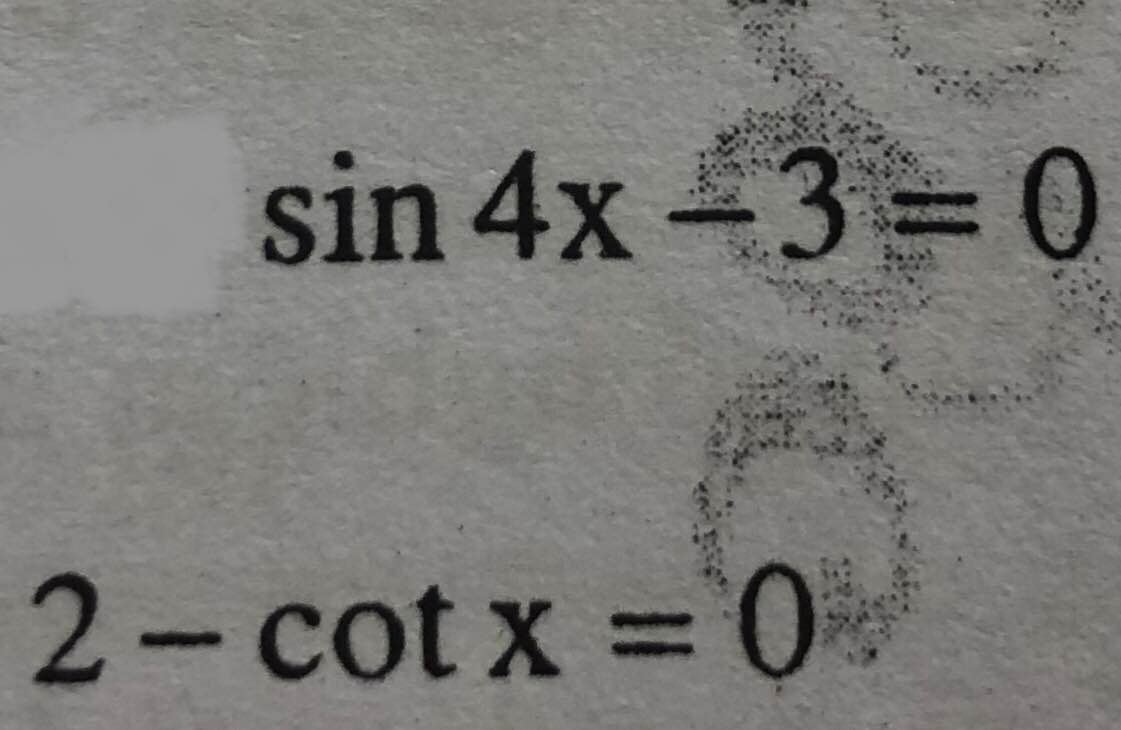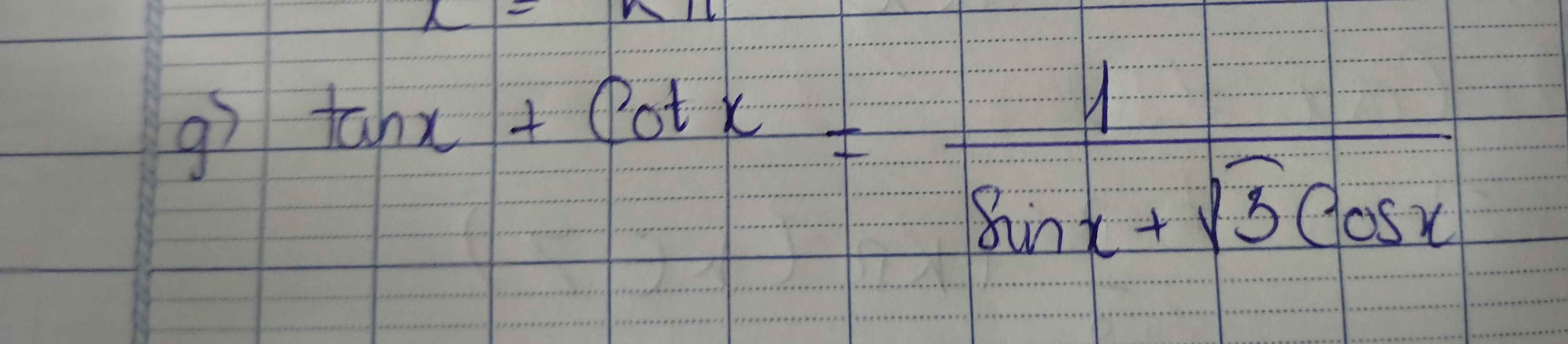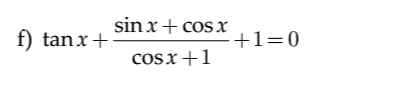15cos2x-11=0
⇔ cos2x=\(\dfrac{11}{15}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=15+k2\pi\\2x=-15+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15}{2}+k\pi\\x=\dfrac{-15}{2}+k\pi\end{matrix}\right.\)
a.
\(15cos2x-11=0\)
\(\Leftrightarrow cos2x=\dfrac{11}{15}\)
\(\Leftrightarrow2x=\pm arccos\left(\dfrac{11}{15}\right)+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{1}{2}arccos\left(\dfrac{11}{15}\right)+k\pi\)
b.
\(2tan4x+1=0\)
\(\Leftrightarrow tan4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=arctan\left(-\dfrac{1}{4}\right)+k\pi\)
\(\Leftrightarrow x=\dfrac{1}{4}arctan\left(-\dfrac{1}{4}\right)+\dfrac{k\pi}{4}\)
c.
\(sin4x-3=0\)
\(\Leftrightarrow sin4x=3>1\)
Vậy pt vô nghiệm
d.
\(2-cotx=0\)
\(\Leftrightarrow cotx=2\)
\(\Leftrightarrow x=arccot\left(2\right)+k\pi\)