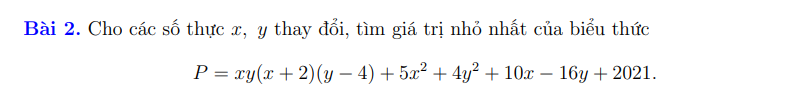Bài 2:
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
b) Ta có: \(B=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-9-\left(x-9\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
c) Để B>1 thì B-1>0
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}-3}{\sqrt{x}-3}>0\)
\(\Leftrightarrow\dfrac{4}{\sqrt{x}-3}>0\)
\(\Leftrightarrow\sqrt{x}>3\)
hay x>9
Bài 2:
d) Để B nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
\(\Leftrightarrow4⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{-2;-1;1;2;4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{1;2;4;5;7\right\}\)
hay \(x\in\left\{1;16;25;49\right\}\)
em ko bt nha chị ơi








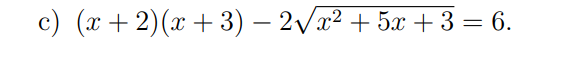 giúp mình với các bạn
giúp mình với các bạn