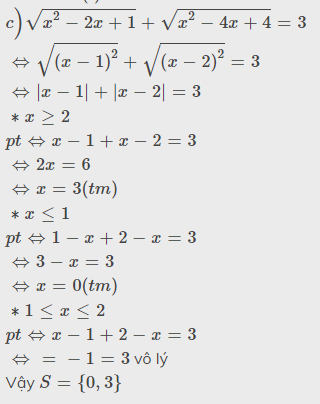Mục đích của việc xét các TH như trên là để phá trị tuyệt đối.
Bạn nhớ rằng, $|x-a|=x-a$ nếu $x\geq a$ và $|x-a|=a-x$ nếu $x< a$
Ta có:
$|x-1|= x-1$ nếu $x\geq 1$
$|x-1|=1-x$ nếu $x< 1$
Và:
$|x-2|=x-2$ nếu $x\geq 2$
$|x-2|=2-x$ nếu $x< 2$
Đến đây ta ghép cặp để xét các TH:
TH1: $x\geq 1$ và $x\geq 2$, tổng hợp lại là $x\geq 2$ (chính là điều kiện 1 trong bài)
TH2: $x\geq 1$ và $x< 2$, tổng hợp lại là $1\leq x< 2$ (chính là điều kiện số 3 trong bài giải mẫu)
TH3: $x< 1$ và $x\geq 2$ (vô lý nên loại, không xét)
TH4: $x< 1$ và $x< 2$, tổng hợp lại là $x< 1$ (chính là điều kiện 2 trong bài). <<Người giải viết $x\leq 1$ cũng không sai, tuy nhiên không nên>>
Bạn đã hiểu chưa nhỉ?