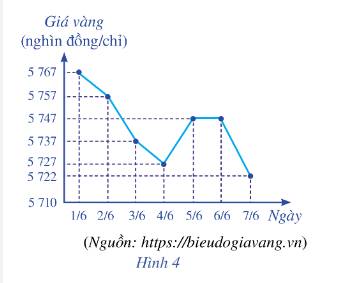
Biểu đồ đoạn thẳng ở Hình 3 biểu diễn tốc độ tăng trưởng GDP của Việt Nam giai đoạn 2012 – 2019.
a) Viết mẫu số liệu thống kê tốc độ tăng trưởng GDP nhận được từ biểu đồ ở Hình 3.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5,25 5,42 5,98 6,68 6,21 6,81 7,08 7,02
b)
+) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5,25 5,42 5,98 6,21 6,68 6,81 7,02 7,08
+) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 7,08 - 5,25 = 1,83\)
c)
+) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5,25 5,42 5,98 6,21 6,68 6,81 7,02 7,08
+) Các tứ phân vị của mẫu số liệu là: \({Q_1} = 5,7,{Q_2} = 6,445,{Q_3} = 6,915\)
+) Khoảng tứ phân vị của mẫu số liệu là: \({Q_3} - {Q_1} = 1,215\)
d)
+) Tốc độ tăng trưởng GDP trung bình của Việt Nam giai đoạn 2012 – 2019 là:\(\overline x = \frac{{5,25{\rm{ + }}5,42{\rm{ + }}5,98{\rm{ + }}6,21{\rm{ + }}6,68\; + 6,81{\rm{ + }}7,02{\rm{ + }}7,08}}{8} = 6,30625\) (%)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5,25 - \overline x } \right)}^2} + {{\left( {5,42 - \overline x } \right)}^2} + ... + {{\left( {7,08 - \overline x } \right)}^2}} \right]}}{8} \approx 0,44\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} \approx 0,66\)(%)